1. Мода (Мо). Модой ДСВ называется ее наивероятнейшее значение. Например, по таблице 2.4: Мо = 1.
Модой НСВ называется значение Х = Мо, соответствующее максимуму плотности вероятности 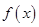 . Для случайной величины в примере 2.4 Мо=4.
. Для случайной величины в примере 2.4 Мо=4.
2. Квантили. Число 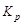 называется р - м квантилем распределения, если оно удовлетворяет уравнению
называется р - м квантилем распределения, если оно удовлетворяет уравнению 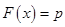 , где
, где 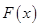 –функция распределения (см. (2.3)).
–функция распределения (см. (2.3)).
Так как 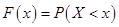 ,
, 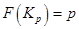 , то
, то 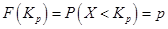 .
.
Таким образом, 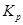 – это точка, левее которой случайная величина попадает с вероятностью р. Для НСВ квантиль Кр может быть найден из уравнения
– это точка, левее которой случайная величина попадает с вероятностью р. Для НСВ квантиль Кр может быть найден из уравнения
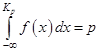
| (3.35) |
(см. свойство 3 плотности вероятности в подразделе 2.5).
Квантили 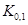 ,
, 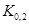 ,...,
,..., 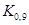 называются децилями. Квантили
называются децилями. Квантили 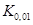 ,
, 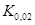 ,...,
,..., 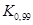 называются процентилями.
называются процентилями.
Пример 2.14. Найдем 25-й процентиль 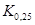 распределения (2.5). По определению
распределения (2.5). По определению 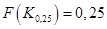 или из (2.20):
или из (2.20):
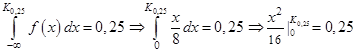
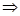
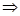
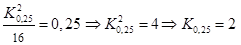 .
.
(отрицательный корень отбрасываем, так как в интервал 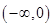 случайная величина X не попадает).
случайная величина X не попадает).
7. Медиана (Ме). Медианой называется половинный квантиль: Ме = 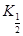 . Очевидно, значения случайной величины X с одинаковой вероятностью 0,5 могут оказаться как левее, так и правее точки X =Ме.
. Очевидно, значения случайной величины X с одинаковой вероятностью 0,5 могут оказаться как левее, так и правее точки X =Ме.
Например, для распределения (2.1) имеем;
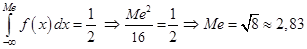
(найдите на графике к примеру 2.4 точки 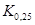 , Ме,
, Ме, 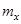 ). Отметин, что для распределений, симметричных относительно
). Отметин, что для распределений, симметричных относительно 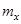 ,
, 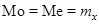 .
.
 2015-06-10
2015-06-10 580
580








