Оптимизация портфеля ценных бумаг. Модель Марковица
Одной из известных моделей оптимизации портфеля ценных бумаг является портфель Марковица минимального риска.
Пусть имеется n-ценных бумаг. Из них инвестор формирует портфель.
Суть задачи состоит в том, чтобы определить такое оптимальное распределение 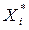 капитала по ценным бумагам, при котором вариация (дисперсия) портфеля минимальна.
капитала по ценным бумагам, при котором вариация (дисперсия) портфеля минимальна.
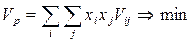 (1)
(1)
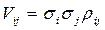
При условии, что обеспечивается заданное значение эффективности портфеля 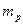 .
.
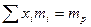 = const (2)
= const (2)
и 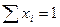 (3)
(3)
Эта задача является задачей на условный экстремум. Алгоритм ее решения следующий:
1) Формируем функцию Лагранжа
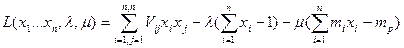 (4)
(4)
Необходимым условием экстремума является равенство нулю ее частных производных по всем переменным.
Вычислив производные функции Лагранжа, получаем:
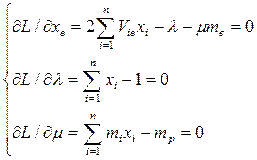
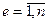
(5)
Решив эту систему n+2 линейных уравнений с n+2 неизвестными (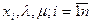 ), получаем оптимальные доли
), получаем оптимальные доли 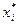 .
.
Пример. Портфель состоит из 3-х видов ценных бумаг, доходности которых являются некоррелированными случайными величинами. Их средние значения и стандартные отклонения равны 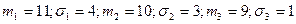 (все величины даны в процентах). Эффективность портфеля
(все величины даны в процентах). Эффективность портфеля 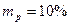 . Определить портфель минимального риска.
. Определить портфель минимального риска.
Решение.
Система (1)-(3) имеет вид:
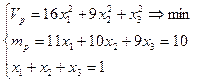
Запишем функцию Лагранжа:
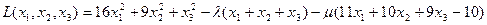
Согласно (5) имеем систему:
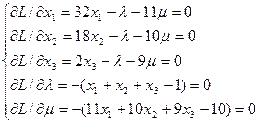
Разрешаем первые 3 уравнения относительно 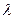 и
и 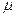
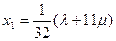 ;
; 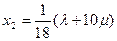 ;
; 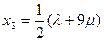
Подставляя эти выражения в последние 2, получаем уравнения для 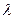 и
и 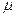
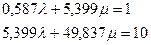
Откуда 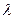 =-45,287;
=-45,287; 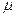 =5,107
=5,107
Подставив эти значения в выражения для Х, получаем оптимальные доли:
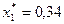 ;
; 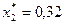 ;
; 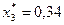
Дисперсия портфеля будет
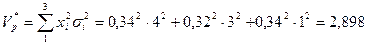
Риск портфеля
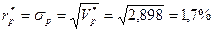
Таким образом, минимальная величина риска 1,7% при доходности 10%.
Общий случай. Домашнее задание
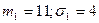 ;
; 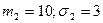 ;
; 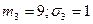
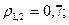
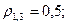
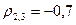
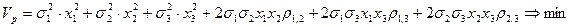 (1)
(1)
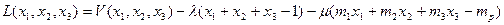
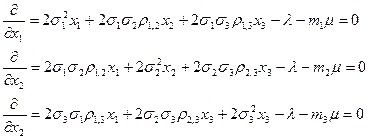
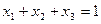
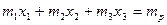
Приходим к системе
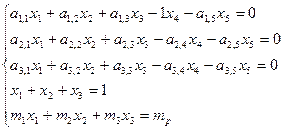
Где 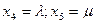
В результате получаем величины 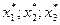 , подставив эти значения в формулу (1) получаем (
, подставив эти значения в формулу (1) получаем (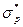 )2 и соответственно
)2 и соответственно 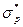 .
.
Таким образом, каждому значению доходности портфеля mp ставится в соответствие минимальная величина риска при соответствующих оптимальных долях.
Задавая различные значения 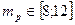 , построить эффективную границу.
, построить эффективную границу.
Безусловное минимальное значение риска
Определим минимальное значение риска без ограничения эффективности портфеля. В этом случае постановка задачи имеет вид:
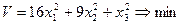 (6)
(6)
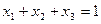 (7)
(7)
Выразим х3 из (7) и подставим в (6).
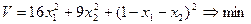
Необходимым условием экстремума является равенство нулю частных производных.
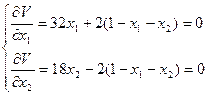
Откуда 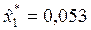 ;
; 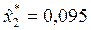 ;
; 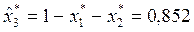
Вариация портфеля
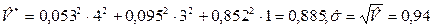
Риск портфеля меньше минимальной волатильности одной бумаги
Эффективность портфеля
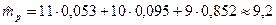
В результате определяем диапазоны изменения параметров портфеля 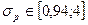
 2015-06-10
2015-06-10 392
392







