Портфель Тобина

Пусть х₀ – безрисковая составляющая с эффективностью σ₀. Ожидаемое значение эффективности портфеля и ее среднеквадратическое отклонение равны:

M_p = x₀∙r₀ + (1 - x₀)∙m_r; σ_p = |1-x₀|∙σ_r (6)

где m_r – эффективность рисковой составляющей портфеля.

Установлено, что x₀ ≤ 1.

Исключая x₀ из системы (6), получаем

σ_p = (m_p – r₀) / (m_r – r₀) ∙σ_r (7)

Изобразим зависимость σ_p от m_p:

Xr =0

Xr =1

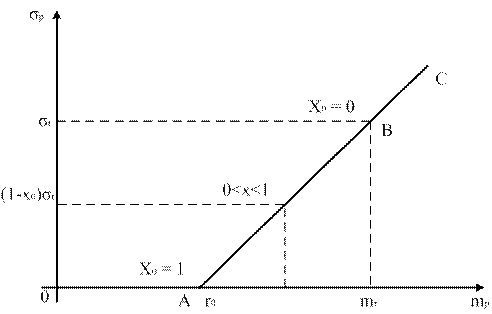
Рис.3

1) при x₀ = 1, весь портфель безрисковый (точка А)

m_p = r₀; σ_p = 0

2) при x₀ = 0; весь портфель рисковый (точка B)

m_p = m_r; σ_p = σ_r

Связь между риском и ожидаемой эффективностью линейная.

С учетом безрисковой компоненты, показатели оптимального портфеля (Тобина) определяются из системы:

V_p = ∑∑x_i∙x_j∙V_ij => min (8)

m_p = r₀∙x₀ + ∑m_j∙x_j (9)

x₀ + ∑x_j = 1 (10)

Построим кривую Марковица (эффективная граница) для рисковой составляющей:

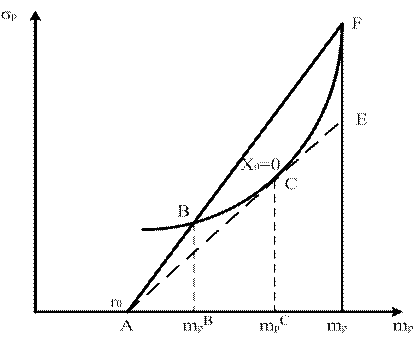
Рис. 1

Рис. 2

Возьмем точку B, на траектории BCF

Пусть x₁^B … x_n^B – пропорции эффективного портфеля B

Очевидно, что x₀ + (1 - x₀) ∑x_j^B = 1

Например х₀=1/3 – доля безрисковой составляющей, а доли рисковых бумаг в рисковой части (точка B) будут x₁=1/5; x₂=4/5 (∑x_i^B=1)

Тогда абсолютные доли рисковых бумаг будут

X₁=(1-x₀)x₁^B=(1-1/3)*1/5= 2/15

X₂=(1-x₀)x₂^B=(1-1/3)*4/5= 8/15

Сумма всех абсолютных долей бумаг в портфеле равна 1, т.е

X₀+(1-X₀)∑X_i^B= 1/3+(1-1/3)*1/5+(1-1/3)*4/5= 1/3+2/15+8/15= 1

r₀∙x₀ + m_p^B(1 - x₀) = r₀∙x₀ + (1 - x₀) ∑m_j∙x_j^B = m_p

Отсюда следует, что портфель (x₀, (1 - x₀) ∙x₁^∙B, …, (1 - x₀) ∙x_n^B) является допустимым то есть траектория AF – одна из допустимых. Но в постановке (8-10) она не эффективна. Так как в диапазоне (m_p^B, m_p^F) она имеет более высокий риск чем на кривой BCE.

Отсюда ясно, что эффективный портфель будет на прямой ACE, которая является касательной к кривой Марковица (эффективной границе), то есть любой заданной эффективности m_p соответствует минимальное значение риска портфеля σ_p.

Пример: Найдем оптимальный портфель Тобина на траектории эффективных комбинаций из двух рисковых бумаг с характеристиками m₁ = 2; σ₁ = 1; m₂=3; σ₂ = 2; ρ_1,2 = 0,5, если эффективность безрискового актива r₀ = 1%.

Решение: Строим кривую Марковица (эффективную границу):

x₁ + x₂ = 1

σ_p² = σ₁²∙x₁² + σ₂²∙x₂² + 2x₁∙x₂∙σ₁∙σ₂ ρ₁

m_p = x₁∙m₁ + m₂∙x₂

σ_p² = 1²∙x₁² + 4x₂² + 2x₁∙x₂∙2∙1/2

m_p = 2x₁ + 3x₂

x₂ = 1 – x₁ → σ_p² = x₁² + 4(1- x₁)² + 2x₁(1- x₁)

m_p = 2x₁ + 3(1 - x₁) = -x₁ + 3 → x₁ = 3 – m_p, откуда

σ_p = √3m_p² – 12m_p +13 (8)

Изобразим кривую на рисунке (для этого найдем контрольные точки):

Найдем σ_{p min} из условия ∂σ_p /∂m_p =(6m_p-12)/ 2√ 3 m_p²-12m_p+13

Точка M

m_p = 2

подставив в (8) найдем σ_pmin

σ_pmin = √34 – 122 + 13 = 1

Получили координаты точки М(m_p^M=2; σ_p^M=1)

Найдем параметры портфеля в точке F:

m_p = 3; x₁ = 0; x₂ = 1

σ_p = √39 – 123 + 13 = √27 + 13 – 36 = 2

Нанесем эти значения на график

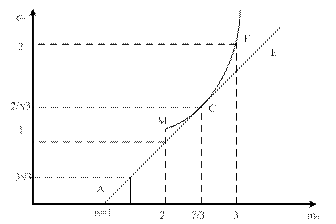
Рис.3

Строим касательную ACE к кривой Марковица. Для этого надо найти координаты точки касания С к графику функции y=f(x). Уравнение касательной к функции y = f(x₀) имеет вид:

y = f(x₀) + f ^’(x₀)(x - x₀) (9)

Здесь аналогом x₀ является m_c, аналогом f(x) является кривая (8)

σ_p(m_c) = √3m_c² – 12m_c +13

σ’_p(m_c) = (6m_c – 12) / (2√3m_c² – 12m_c + 13), откуда

σ_p = √3m_c² – 12m_c +13 + (3m_c – 6) / √3m_c² – 12m_c +13 ∙ (m_p – m_e)

Эта прямая проходит через A (1; 0), откуда получаем уравнение:

0 = √3m_c² – 12m_c + 13 + (3m_c-6) / √3m_c² – 12m_c + 13 (1 – m_c)

Решив это уравнение получаем m_c = 7/3. Подставив m_c = 7/3 в (8) получаем:

σ_с = √3(7/3)² – 12(7/3) + 13 = 2/√3, откуда

x₁* = 3 – m_c = 3 – 7/3 = 2/3

x₂* = 1 – 2/3 = 1/3

Получаем оптимальную структуру рисковой части портфеля.

Как видим из решения, структура рисковой части оптимального портфеля не зависит от склонности инвестора к риску (от x₀).

Пусть доля безрисковых бумаг x₀ = 1/3, тогда доли рисковых частей будут равны:

x₁ = (1 – x₀)x₁* = (1 – 1/3) ∙ 2/3 = 4/9

x₂ = (1 – x₀)x₂* = (1-1/3) ∙ 1/3 = 2/9

В результате эффективность портфеля, содержащего безрисковую компоненту:

m_p = 1/3*1 + 4/9*2 + 2/9*3 = 1/3 + 8/9 + 6/9 = 17/9

σ_p = |1-x₀| ∙ σ_r = (1-1/3) * (2/√3) = 4/(3√3)

В результате определили оптимальные доли портфеля Тобина, его эффективность и риск (точка C на рис 3).

В том случае, если портфель в рисковой части содержит более 2 ценных бумаг, то по заданным значениям эффективности портфеля mp определяем оптимальные доли x_i*, I = 1,n, обеспечивающие минимальный риск. Для найденных долей x_i^* находим σ_{p min}. В результате каждому значению m_p ставим в соответсвие σ_{p min.} По найденным долям x_i* находим σ_p*_min. В результате каждому значению m_p ставим в соответствие σ_{p min.} По найденным значениям σ_r от m_p строим кривую Марковица (эффективную границу). Затем для заданного значений r₀ строим касательную к кривой Марковица. Определяем величины m_p^c и σ_p^с в точке касания. Для полученного значения mc определяем оптимальные доли рисковой части портфеля x₁*, … x_n*. В итоге получаем оптимальные доли портфеля Тобина минимального риска:

x₀*, |1-x₀|x₁*, …, |1-x₀|x_n *

Д.З.: Построить касательный портфель к эффективной границе (при r=1).

Вывод:

1. Структура рисковой части портфеля не зависит от склонности инвестора к риску (склонность к риску определяется безрисковой долей x_0, если x₀=0, то портфель абсолютно рисковый, если x₀=1, то портфель абсолютно безрисковый);

2. Если инвестор интересуется только ожидаемой доходностью и стандартным отклонением своего портфеля, то он будет комплектовать портфель только из «касательного» (оптимального) портфеля С и безрискового актива.