Локальная теорема Муавра-Лапласа

Если вероятность «успеха» р, 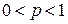, при одном испытании в 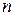независимых испытаниях Бернулли не зависит от числа испытаний 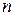, то для ,

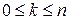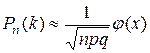, (4.3)

где 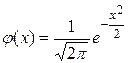, а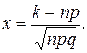

Значения функции 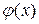приведены в приложении 2.

Интегральная теорема Муавра-Лапласа.

Если вероятность «успеха» р, 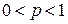, при одном испытании в 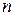независимых испытаниях Бернулли не зависит от числа испытаний 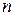, то для любых целых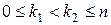

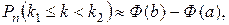(4.3)

где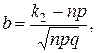

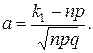
Значения функции 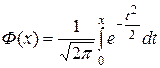приведены в приложении 1.

Теорема (Бернулли). Пусть вероятность «успеха» р, 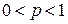, при одном испытании в 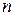независимых испытаниях Бернулли не зависит от числа испытаний .

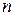При достаточно большом 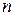для любого 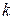, 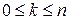и любого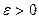

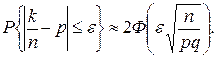(4.4)

Отношение 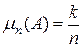называется относительной частотой появления события 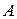, (т.е. «успеха») при 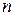независимых испытаниях.

Замечание. Теорема Пуассона используется обычно пр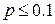и и 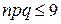. В случае, когда 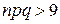, используют предельные теоремы Муавра-Лапласа (см.: Хельд А. Математическая статистика. М., ил. 1956. С. 585).