Пусть 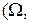
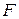 ,
, 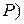 - вероятностное пространство,
- вероятностное пространство, 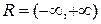 –множество действительных чисел.
–множество действительных чисел.
Определение. Случайной величиной называется действительная функция 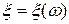 , (
, (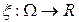 ) такая, что для каждого действительного
) такая, что для каждого действительного 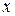
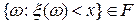 .
.
Напомним, что 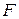 –
– 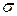 -алгебра событий, то есть
-алгебра событий, то есть 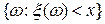 – некоторое событие вероятностного пространства.
– некоторое событие вероятностного пространства.
Определение. Функция
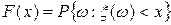 (5.1)
(5.1)
называется функцией распределения вероятностей случайной величины 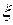 .
.
Свойства функции распределения вероятностей:
1. 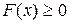 для любого
для любого 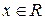 ;
;
2. 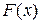 - неубывающая, непрерывная слева;
- неубывающая, непрерывная слева;
3. 
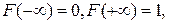 т.е.
т.е. 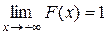 ,
, 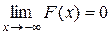 ;
;
4. 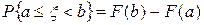 .
.
Определение. Случайные величины 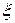 и
и 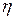 называются независимыми, если при любых действительных
называются независимыми, если при любых действительных 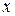 и
и 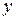 имеет место
имеет место
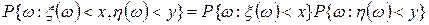 .
.
К основным числовым характеристикам случайных величин относят математическое ожидание, дисперсию и среднее квадратическое отклонение.
Определение. Математическим ожиданием дискретной случайной величины 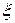 называется число
называется число
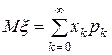 , (5.2)
, (5.2)
(при условии, что ряд сходится). Здесь 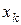 –значения случайной величины
–значения случайной величины 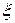 ,
, 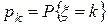 –вероятность, с которой случайная величина
–вероятность, с которой случайная величина 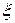 принимает значение
принимает значение 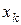 .
.
Свойства математического ожидания.
1. Если 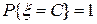 , то
, то 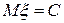 . Иначе
. Иначе 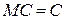 , где
, где 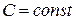 .
.
2. 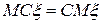 , где
, где 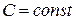 .
.
3. 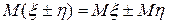 .
.
4. Если случайные величины 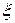 и
и 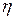 независимы, то
независимы, то 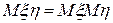 .
.
Определение. Математическим ожиданием дискретной случайной величины 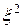 называется число
называется число
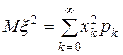 , (5.3)
, (5.3)
(при условии, что ряд сходится).
Определение. Дисперсией случайной величины 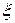 называется число
называется число
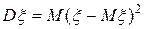 , (5.4)
, (5.4)
Свойства дисперсии.
0. 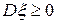 .
.
1. Если 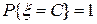 , то
, то 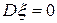 . Иначе
. Иначе 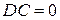 , где
, где 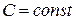 .
.
2. 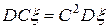 , где
, где 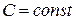 .
.
3. Если случайные величины 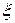 и
и 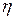 независимы, то
независимы, то
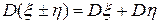 .
.
4. 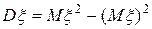 .
.
Определение. Средним квадратическим отклонением случайной величины называют величину 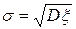 .
.
 2015-06-10
2015-06-10 715
715








