Глава 6. Непрерывные случайные величины и их характеристики

Определение. Случайная величина 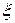называется абсолютно-непрерывной, если существует такая неотрицательная функция 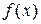, что при любом действительном 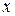справедливо представление

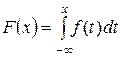. (6.1)

Определение. Функция 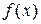называется функцией плотности распределения вероятностей случайной величины 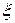и обладает свойствами

1. При любом .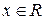

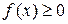2. При почти всех 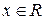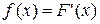. (6.2)

3. .

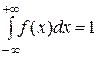Определение. Математическим ожиданием дискретной случайной величины 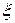называется число

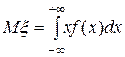, (6.3)

(при условии, что соответствующий интеграл существует).

Определение. Математическим ожиданием дискретной случайной величины 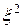называется число

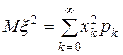. (6.4)

Все свойства функции распределения вероятностей, математического ожидания, определение и свойства дисперсии сохраняются.