События 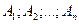 попарно независимы, если в любой паре
попарно независимы, если в любой паре 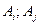 события
события 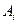 и
и 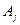 независимы.
независимы.
Независимость в совокупности и попарная независимость событий – понятия разные.
Пример.
Три грани треугольной пирамиды окрашены соответственно в белый, зеленый, желтый цвета. На последней грани присутствуют все три цвета. Случайным образом выбирают грань.
Найти вероятности событий: 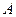 =«на грани есть желтый цвет»;
=«на грани есть желтый цвет»; 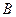 =«на грани есть белый цвет»;
=«на грани есть белый цвет»; 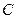 =«на грани есть зеленый цвет»;
=«на грани есть зеленый цвет»;
Решение.
Желтый цвет имеется на двух гранях из четырех, т.о. 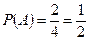 ; аналогично:
; аналогично: 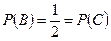 .
.
Вероятность того, что на выпавшей грани есть два цвета - 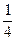 , т.е.
, т.е. 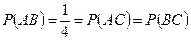 .
.
Таким образом,
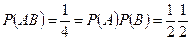
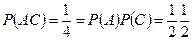
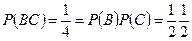 ,
,
Т.е. все события попарно независимы. Однако события не являются независимыми в совокупности:
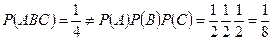
Теорема. (О появлении хотя бы одного из независимых событий)
Пусть вероятность появления каждого из п событий 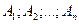 , независимых в совокупности, равна
, независимых в совокупности, равна 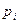 . Вероятность появления хотя бы одного события, равна
. Вероятность появления хотя бы одного события, равна
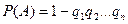 ,
, 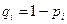
Доказательство.
Поскольку по закону Де Моргана 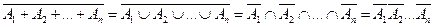 ,
,
То 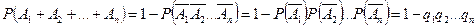 .
.
 2015-06-10
2015-06-10 490
490








