Пример. В группе 20 студентов. Из них двое курят, 12 – в очках, 6 – курят и носят очки

В группе 20 студентов. Из них двое курят, 12 – в очках, 6 – курят и носят очки. Найти вероятность того, что студент курит, если он носит очки.

Решение.

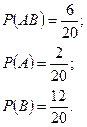Пусть событие - студент курит; - студент носит очки.

Тогда

.

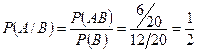Заметим, что условная и безусловная вероятности события 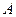в данной задаче различны: .

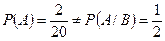События называются независимыми, если появление одного из них не влияет на вероятность появления другого: .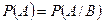

Если события независимые, то теорема умножения вероятностей принимает вид:

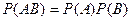- критерий независимости событий.

В рассмотренном примере события 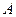и 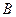- зависимы, поскольку

.

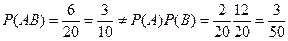Пример.

Бросают три монетки и игральную кость. Событие 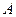- выпал герб, событие 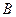- выпало число очков, равное 6. Пространством элементарных исходов опыта является множество 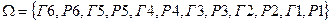. Тогда , , .

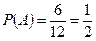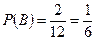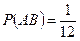Таким образом, 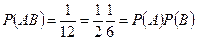, т.е. события 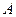и 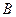- независимы.

Свойства независимых событий