Пример решения задачи симплексным методом

Торговое предприятие, располагающее материально-денежными ресурсами, реализует три группы товаров А, В и С. Плановые нормативы затрат ресурсов на тыс. руб. товарооборота, прибыль от продажи товаров на тыс. руб. товарооборота, а также объем ресурсов заданы в таблице 2.

Определить плановый объем продажи и структуру товарооборота так, чтобы прибыль торгового предприятия была максимальной.

Таблица 2

Виды материально-денежных ресурсов	Норма затрат материально-денежных ресурсов на ед. товарооборота, тыс. руб.	Объём ресурсов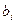
А _ группа _	В группа	С группа
Рабочее время продавцов, чел./ч	0,1	0,2	0,4
Площадь торговых залов, м²	0,05	0,02	0,02
Площадь складских помещений, м²
Прибыль, тыс.руб.				max

1. Запишем математическую модель задачи.

Определить 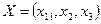, который удовлетворяет условиям

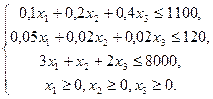
и обеспечивают максимальное значение целевой функции

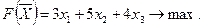
Для построения первого опорного плана систему неравенств, приведем к системе уравнений.

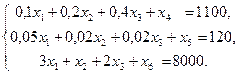
В матрице этой системы уравнений имеет:

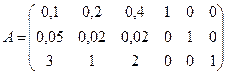
Векторы - линейно независимы, так как определитель, составленный из компонент этих векторов, отличен от нуля:

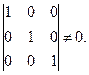
Соответствующие этим векторам переменные 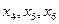будут базисными.

Решим систему уравнений относительно базисных переменных.

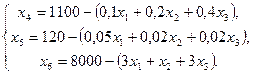
Функцию цели запишем в виде:

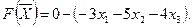
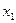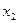2. Полагая, что свободные переменные =0, =0, 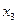=0, получим первый опорный план

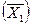=(0,0,01100,120,8000), F = 0, в котором базисные переменные 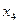=1100, 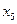=120, 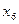=8000,

следовательно товары не продаются и прибыль равна нулю, а ресурсы не используются.

Заносим первый опорный план 1 в симплексную таблицу.

План	Базисные переменные	Ресурсы плана	Значения коэффициентов при переменных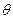

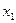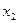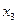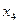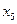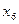I план		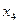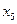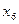1100 120 8000	0,1 0,05 3	0,2 0,02 1	0,4 0,02 2		0 1 0
Инд. Строка		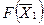	-3	-5	-4
II план		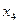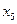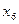5500 10 2500	0,5 0,04 2,5		-0,02 0	-0,1 -5
Инд. Строка		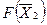	-0,5
III план		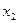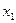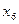5375 250 1 875			2,25 -0,5 1,25	6,25 -2,5 1,25	-12,5 25 -62,5	0 0
Инд. строка		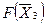			5,75	23,75	12,5

Симплексная таблица

Первый опорный план 1 не оптимальный, так как в индексной строке находятся отрицательные коэффициенты - -3,-5,-4.

За ведущий столбец выберем столбец, соответствующий переменной 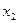, так как сравнивая по модулю имеем:

|- 5| > 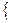|- 3I, |- 4I} Рассчитываем значения 9 по строкам, как частное от деления 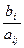и выбираем наименьшее:

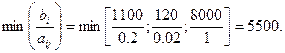
Следовательно, первая строка является ведущей.

Разрешающий элемент равен 0,2 и находится на пересечении ведущего столбца и ведущей строки и выделен кругом.

3. Формируем следующую симплексную таблицу. Вместо переменной 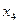в план II войдет переменная 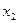. Строка, соответствующая переменной 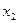в плане II, получена в результате деления всех элементов строки 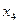плана I на разрешающий элемент 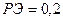. На месте разрешающего элемента в плане II получаем 1. В остальных клетках столбца 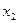плана II записываем нули.

Таким образом в новом плане II заполнены строки 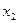и столбец 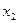. Все остальные элементы нового плана II, включая элементы индексной строки определяется по правилу прямоугольника. Для этого выбираем из старого плана 4 числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент 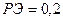. Во второй вершине по диагонали находится старое значение элемента, например, значение целевой функции 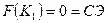, которое указывает на место расположение нового 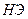в новом плане II. Третий элемент А =1100 и четвертый элемент В =-5 завершают построение прямоугольника в недостающих двух вершинах и расположены по другой диагонали. Значение нового элемента в плане II находится из выражения:

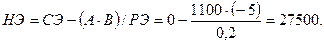
Элементы строки определяются аналогично:

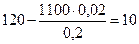
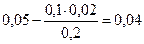
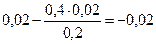
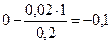
Все элементы, расположенные на пересечении строк и столбцов, соответствующих одновременным базисным элементам равны 1, остальные элементы столбца в базисах векторов, включая индексную строку, равны 0. Аналогично проводятся расчеты по всем строкам таблицы, включая индексную.

Выполняя последовательно веб этапы алгоритма, формируем план II.

4. На третьей интеракции таблицы 3 получаем план III, который является оптимальным, так как все коэффициенты в индексной строке 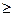0.

Оптимальный план можно записать так:

X = (250,5375,0,0,0,1875), 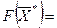27625 тыс. руб.

Следовательно, необходимо продавать товаров первой группы А 250 ед., а второй группы В - 5375 ед. При этом торговое предприятие получает максимальную прибыль в размере 27625 тыс. руб. Товары группы С не реализуются.

"В оптимальном плане среди базисных переменных находится дополнительная переменная 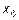.Это указывает, что ресурсы третьего вида (площадь складских помещений) недоиспользована на 1875 м², так как переменная 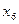была введена в третье ограничение задачи, характеризующее собой использование складских помещений.

В индексной строке оптимального плана в столбцах переменных 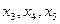не вошедших в состав базисных, получены ненулевые элементы, поэтому оптимальный план задачи линейного программирования является единственным.