2015-06-10
396
Рассмотрим платежную матрицу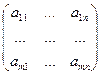 
и случай, когда 
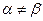и все элементы 
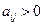(с помощью преобразований любую матрицу можно привести к такому виду), тогда и цена игры 
.
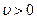Найдем оптимальную смешанную стратегию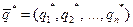 
игрока В. Применяя ее, игрок В проиграет не более υ при любой чистой стратегии игрока А.
Найти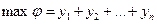 
при ограничениях 
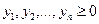
Это типичная задача линейного программирования, записанная в симметричной форме. Решив ее, найдем оптимальной решение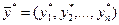 
и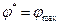 
. Для определения цены игры применяем формулу 
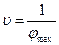, компоненты оптимальной смешанной стратегии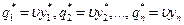 
Рассуждая аналогично для игрока А, придем к задаче №2:
Найти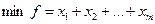 
при ограничениях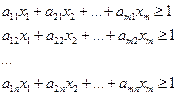 
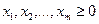
Решая эту задачу, найдем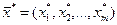 
и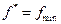 
, а затем 
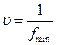и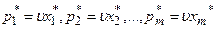 
.
Задачи №1 и №2 образуют пару симметричных двойственных задач линейного программирования, поэтому достаточно найти решение одной из них.
