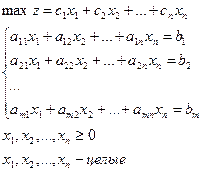Пусть дана полностью ЦЗЛП

(*)

1) Отбросив условие целочисленности, решим исходную задачу симплексным методом.

Пусть на последнем шаге симплексного метода получили таблицу:

i	БП	C б	b i		…		…			…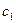
			…			…
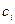
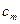
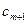
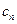
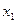
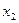
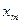
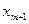
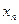
… i … m	… …	… …	… …	… …		… …	…	… …	… …	…	… …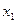
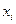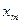
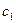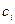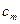
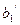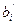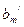
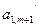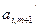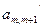
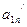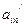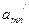
m+1							…			…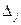

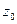
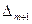
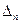
Этой таблице соответствует система ограничений

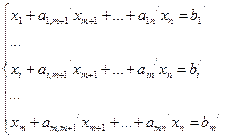
Оптимальное решение имеет вид (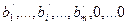). Если получится целочисленное оптимальное решение, то задача решена. Если в оптимальном решении не все переменные целочисленные, то строим сечение.

2) Пусть в оптимальном решении переменная 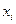= 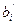, где 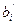и хотя бы один из коэффициентов 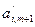,…, 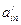являются дробными числами. Выписываем уравнение, содержащее переменную :

.

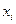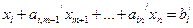Для этого уравнения строим неравенство 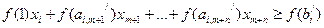, где 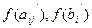- дробные части чисел.

3) Присоединяя неравенство к ранее решенной задачи, получим новую задачу линейного программирования, которую решаем двойственным симплексным методом; если ее оптимальное решение окажется целочисленным, то оно и будет оптимальным решением исходной задачи. Если снова получится нецелочисленное решение, то строим новое сечение и т.д.