Формально задача потребительского выбора имеет вид:
найти 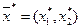 такой, что
такой, что 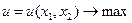
при условиях 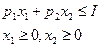
Как известно для решения задачи на условный экстремум применяется методом множителей Лагранжа.
1) Составим функцию Лагранжа
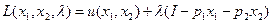
где λ – множитель Лагранжа. Найдем первые частные производные функции Лагранжа по переменным 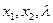 и приравниваем эти частные производные к нулю
и приравниваем эти частные производные к нулю 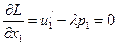 ,
, 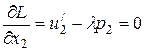 ,
, 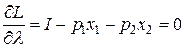 .
.
2) Составим и решим систему 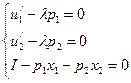
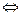
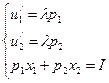 раздели первое уравнение на второе для того, чтобы исключить вспомогательную переменную
раздели первое уравнение на второе для того, чтобы исключить вспомогательную переменную 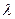 ,
, 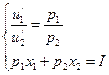
Решение 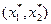 системы является решением задачи потребительского выбора.
системы является решением задачи потребительского выбора.
Пример. Решить задачу потребительского выбора, определив функции спроса. Цены товаров р 1=10, р 2=2 и доходе I =60 с функцией предпочтения u = x 1 x 2 →max.
1) Составим функцию Лагранжа L (x 1, x 2,λ)= x 1 x 2 + λ (I - p 1 x 1- p 2 x 2)
2) Найдем первые частные производные функции Лагранжа по переменным 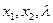 и приравниваем эти частные производные к нулю
и приравниваем эти частные производные к нулю
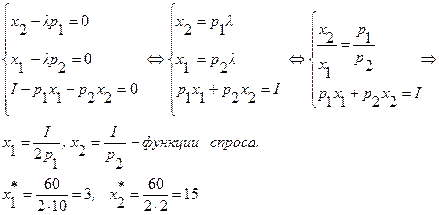
 2015-06-10
2015-06-10 1444
1444








