2015-06-10
959
Принцип оптимальности (основное правило динамического программирования): Каково бы ни было начальное состояние системы на любом шаге и управление, выбранное на этом шаге, последующие управления должны выбираться оптимальными относительно состояния, к которому придет система в конце данного шага.
Пусть процесс имеет n шагов. Состояние системы на каждом шаге i описывается s параметрами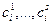 
, которые называются фазовыми координатами. Введем обозначения:
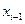- множество состояний системы S перед шагом i (
);
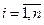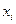- множество состояний системы S в конце шага i();
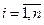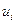- множество управлений, которые возможно выбрать на шаге i и под воздействием каждого из которых система S переходит в одно из состояний множества ();
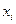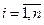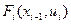- условно-оптимальное значение целевой функции от шага i до шага n, при условии, что перед шагом i система S находилась в одном из состояний множества 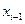; а на шаге i было выбрано управление 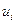, обеспечивающее целевой функции условно-оптимальное значение;
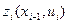- значение целевой функции (показатель эффективности) на шаге i для всех управлений из множества 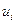при условии, что на шаге i система S находилась в одном из состояний множества ;
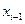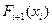- условно-оптимальное значение целевой функции от шага i+ 1 до шага n, при условии, что в результате воздействия управления, выбранного из множества 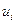, система S на шаге i перейдет из состояния, принадлежащего множеству 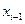, в одно из состояний множества (
).
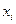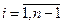Формально принцип оптимальности Беллмана имеет вид:
= 
( + ) (*).
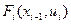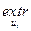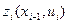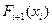Уравнение (*) называется основным функциональным уравнением динамического программирования (или уравнением Беллмана, или рекуррентными соотношениями).
Рассмотрим последний шаг n процесса и уравнение (*):
= (
+ 
).
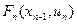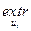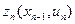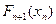Функция 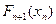не определена при 
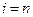, значит, 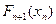=0. Получим
=
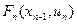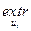
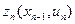
В процессе условной оптимизации по уравнениям Беллмана (рекуррентным соотношениям) определяются условно-оптимальные значения целевой функции и оптимальные управления для всех возможных состояний системы на каждом шаге, начиная с последнего.
После определения значений функции 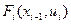и соответствующих оптимальных управлений для всех шагов от шага n до шага 1 переходят к безусловной оптимизации. По известному начальному состоянию системы для 1-го шага определяют оптимальный результат за следующие n шагов (
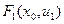) и управление 
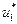на шаге 1, которое обеспечивает этот результат. Применяя управление 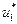система перейдет в определенное состояние из множества 
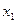, зная которое возможно определить 
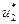и так далее до последнего шага n.
