Непрерывная случайная величина
Определение: Непрерывной называют величину, все возможные значения которой полностью заполняют конечный или бесконечный промежуток числовой оси.
Очевидно, число возможных значений непрерывной случайной величины бесконечно.Непрерывную случайную величину можно задавать с помощью функции распределения.
Определение: Функцией распределения непрерывной случайной величины Х называется функция F(х), определяющая для каждого значения х 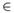 R
R
вероятность того, что случайная величины Х в результате испытания примет значение, меньшее х:F(x)=P(X<x),где х 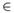 R
R
Функцию распределения иногда называют интегральной функцией распределения.
Свойства функции распределения:
1)1≤ F(x) ≤1
2)У непрерывной случайной величины функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.
3) Вероятность попадания случайной величины Х в один из промежутков (а;b), [а;b), [а;b], равна разности значений функции F(х) в точках а и b,т.е. Р(а<Х<b)= F(b)- F(a)
4)Вероятность того, что непрерывная случайная величина Х примет одно отдельное значение равна 0.
5) F(-∞)=0, F(+∞)=1
Задание непрерывной случайной величины с помощью функции распределения не является единственным.
Плотность распределения неправильной и свойства плотности распределения.
Определение: Плотностью распределения вероятностей f(x) непрерывной случайной величины Х называется производная от ее функции распределения, т.е.:
f(x)=F’(x)
Плотность распределения вероятностей иногда называют дифференциальной функцией распределения или дифференциальным законом распределения.
График плотности распределения вероятностей f(x) называется кривой распределения вероятностей.
Свойства плотности распределения вероятностей:
1)f(x) ≥0,при х 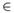 R
R
х
2) F(x)= ∫ f(x)dx
-∞
Геометрически функция распределения равна площади фигуры, ограниченной сверху кривой распределения снизу осью ОХ и лежащей левее точки х (рис.1)
b
3) Р(а<Х<b)= ∫ f(x)dx
a
Геометрически полученная вероятность равна площади криволинейной трапеции, ограниченной сверху кривой распределения, снизу осью ОХ, слева и справа прямыми х=а, х=b (рис. 2)
-∞
4) ∫ f(x) dx=1-условие нормировки
+∞
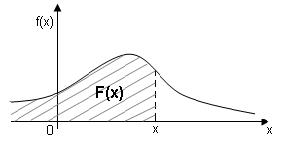
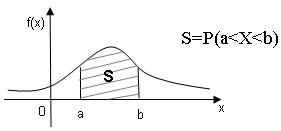
рис.1 рис.2
 2015-06-11
2015-06-11 409
409








