Выделим в «абсолютно» покоящейся жидкости произвольные точки 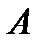 и
и 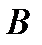 с координатами
с координатами 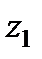 и
и 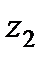 (рис. 2.9). Удалив из трубок с запаянными верхними концами воздух, погрузим их отвесно в жидкость так, чтобы нижние открытые их концы совпали с точками
(рис. 2.9). Удалив из трубок с запаянными верхними концами воздух, погрузим их отвесно в жидкость так, чтобы нижние открытые их концы совпали с точками 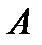 и
и 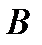 .
.
Под действием разности давлений жидкость в трубках поднимется до точек 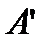 и
и 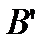 . Давление в этих точках полагается равным нулю (хотя в действительности оно будет несколько выше нуля за счет упругости паров жидкости и остаточного воздуха в концах трубки).
. Давление в этих точках полагается равным нулю (хотя в действительности оно будет несколько выше нуля за счет упругости паров жидкости и остаточного воздуха в концах трубки).
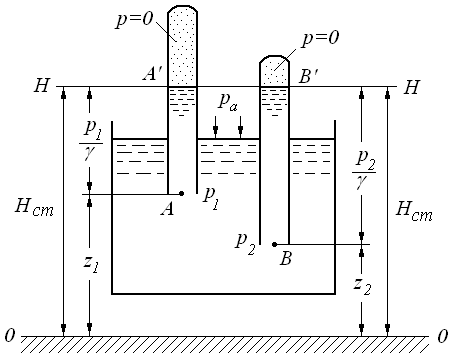
Рис.2.9. Закон распределения давления
в «абсолютно» покоящейся жидкости
Применим основное уравнение гидростатики (2.10) к точкам 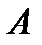 и
и 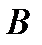
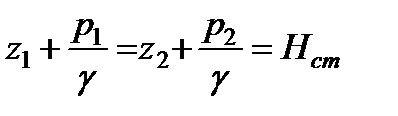 .
.
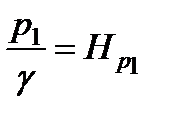 и
и 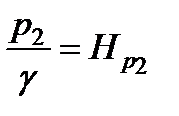 - это высоты столбов жидкости в трубках, измеренные относительно точек
- это высоты столбов жидкости в трубках, измеренные относительно точек  и
и  . Таким образом, точки
. Таким образом, точки 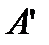 и
и 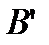 лежат в одной горизонтальной плоскости. Высота для любой точки жидкости над плоскостью
лежат в одной горизонтальной плоскости. Высота для любой точки жидкости над плоскостью  равна сумме высот
равна сумме высот
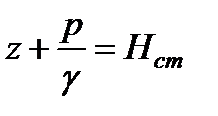 . (2.18)
. (2.18)
В итоге приходим к выводу, что каждый из членов уравнения (2.18) представляет собой некоторую высоту, которым присвоены определенные названия:
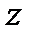 - геометрическая (или нивелирная) высота;
- геометрическая (или нивелирная) высота;
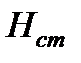 - высота полного гидростатического напора.
- высота полного гидростатического напора.
Геометрический смысл основного уравнения гидростатики. Сумма геометрической 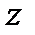 и пьезометрической высоты
и пьезометрической высоты 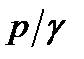 равна полному гидростатическому напору
равна полному гидростатическому напору 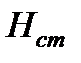 и есть величина постоянная для всех точек данной покоящейся массы жидкости. Пьезометрическая высота
и есть величина постоянная для всех точек данной покоящейся массы жидкости. Пьезометрическая высота 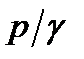 (а с ней и гидростатическое давление
(а с ней и гидростатическое давление 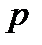 ) может изменяться только ха счёт соответствующего изменения геометрической высоты
) может изменяться только ха счёт соответствующего изменения геометрической высоты 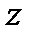 , т.е. при увеличении
, т.е. при увеличении 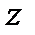 уменьшается
уменьшается 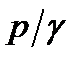 , и наоборот.
, и наоборот.
 2015-06-04
2015-06-04 747
747

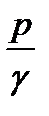 -
- 






