2015-06-04
686
Рассмотрим потенциальную энергию жидкости в элементарном объёме, выделенном около произвольной точки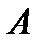 
с геометрической высотой 
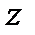и давлением 
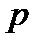(рис. 2.10).
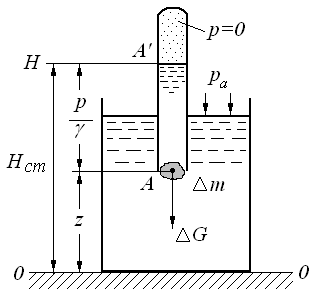
Рис. 2.10. Энергетическая интерпретация
основного уравнения гидростатики
Полная потенциальная энергия в этом объёме складывается из двух частей: потенциальной энергии положения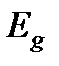 
и потенциальной энергии давления 
:
.
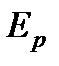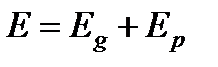Первая из них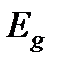 
может быть определена как работа, которую совершила бы сила тяжести 
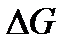при опускании массы выделенного объёма жидкости 
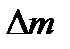до уровня плоскости сравнения 
:
.
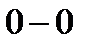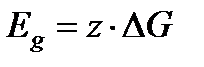Вторая же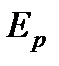 
может быть превращена в механическую работу, на которую можно поднять жидкость, если в точку 
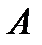опустить запаянную с одного конца трубку с удаленным из неё воздухом. Как мы уже знаем, жидкость поднимется в такой трубке на высоту 
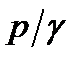, следовательно, жидкость, обладая весом 
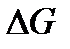, совершит работу 
.
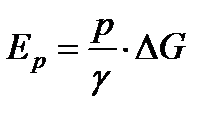Таким образом, потенциальная энергия выделенной частицы жидкости
.
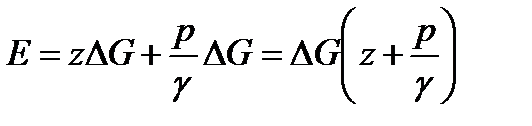Отнеся потенциальную энергию к весу жидкости, получим высоту полного гидростатического напора:
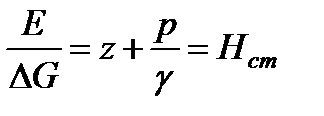. (2.19)
Как видим, каждый из членов уравнения (2.19) представляет собой удельную (приходящуюся на единицу веса жидкости) энергию того или иного вида:
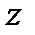- удельная потенциальная энергия положения жидкости;
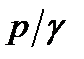- удельная потенциальная энергия давления;
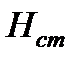- полная удельная потенциальная энергия покоящейся жидкости.
Энергетический смысл основного уравнения гидростатики. Сумма удельной потенциальной энергии положения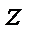 
и удельной потенциальной энергии давления 
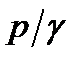равна полной удельной потенциальной энергии 
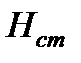и есть величина постоянная для всех точек данной покоящейся массы жидкости.
Удельная потенциальная энергии давления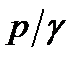 
может изменяться только ха счёт изменения удельной потенциальной энергия положения жидкости 
.
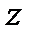Закон распределения давления в (2.19) можно таким образом рассматривать как частное выражение закона сохранения энергии применительно к непрерывному объёму «абсолютно» покоящейся несжимаемой жидкости, когда один вид энергии переходит в другой, и наоборот.
