2015-06-04
2978
Пусть жидкость находится в абсолютном равновесии в поле земного тяготения, т.е. когда на жидкость действует только сила тяжести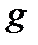 
, а ось 
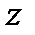направленавверх (рис. 2.7).
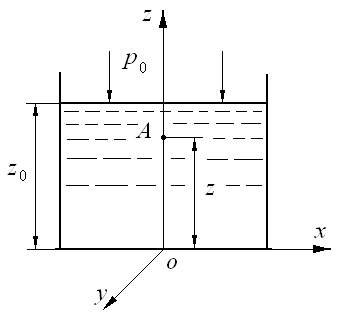
Рис. 2.7. Равновесие в поле земного тяготения
Запишем проекции единичных массовых сил на оси координат
, 
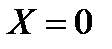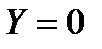и 
.
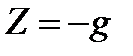Подставим эти значения в основное уравнение гидростатики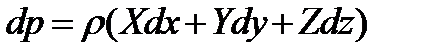 
.
Следовательно, для этого частного случая равновесия жидкости получим
. (2.13)
Но произведени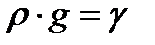е 
, где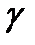 
- удельный вес жидкости.
Делая подстановку и деля обе части уравнения (2.13) на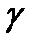 
запишем уравнение в следующем виде
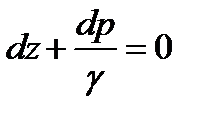
После интегрирования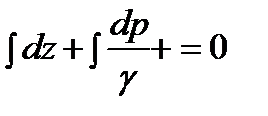 
будем иметь
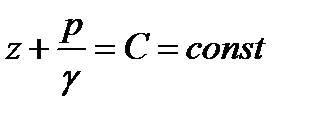. (2.14)
Или обозначив эту сумму через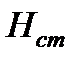 
, получим
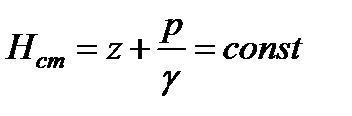(2.15)
Уравнение (2.15) представляет собой основное уравнение гидростатики, полученное путем интегрирования дифференциального уравнения Эйлера.Это и есть закон распределения давления в «абсолютно» покоящейся жидкости: чем меньше координата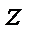 
, т.е. чем глубже погружена та или иная точка, тем больше давление 
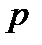в этой точке.
Закон распределения гидростатического давления (2.15) может быть представлено в другой форме. Определим постоянную интегрирования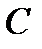 
, используя граничные условия для точки 
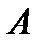, лежащей на свободной поверхности, т.е. 
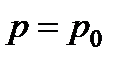и 
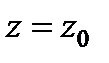. Подставляя эти значения в (2.14), находим
|
|
|
.
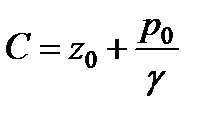Подставив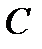 
в уравнение (2.14), получим
,
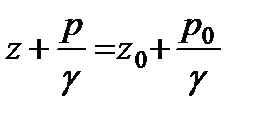или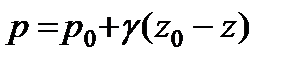 
. (2.16)
Заменив в уравнении (1.16)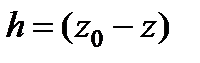 
, где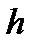 
- глубина расположения точки, найдем
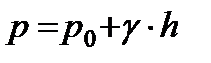, (2.17)
где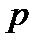 
- абсолютное давление; 
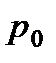- давление на свободной поверхности; 
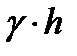- избыточное гидростатическое давление в рассматриваемой точке.
Как ясно из формул (2.16) и (2.17), гидростатическое давление линейно зависит от глубины погружения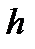 
: чем больше глубина 
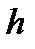, тем больше давление 
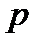в данной точке.
Этот линейный закон распределения давления может быть изображен графически в виде эпюр абсолютного или избыточного давления (рис.2.8).
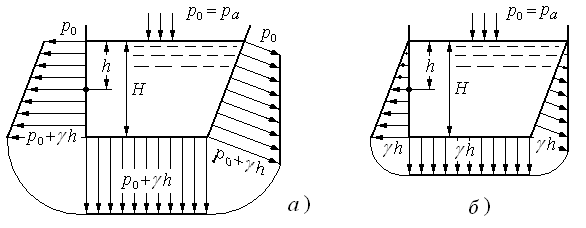
а – абсолютного; б - избыточного
Рис. 2.8. Эпюры гидростатического давления
