2015-06-04
698
Описанный выше прием нахождения вертикальной составляющей силы давления жидкости на криволинейную стенку используют для доказательства закона Архимеда. Пусть в жидкость погружено тело произвольной формы объемом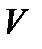 
(рис. 2.18).
Спроектируем его сечение на свободную поверхность жидкости и проведем проектирующую цилиндрическую поверхность, которая касается поверхности тела по замкнутой кривой. Эта кривая отделяет верхнюю часть поверхности тела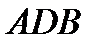 
от нижней ее части 
.
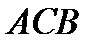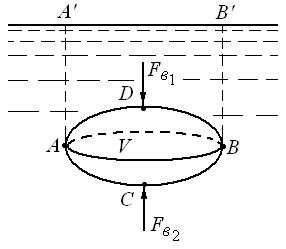
Рис. 2.18. Схема для доказательства закона Архимеда
Вертикальная составляющая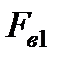 
силы избыточного давления жидкости на верхнюю часть поверхности тела направлена вниз и равна весу жидкости в объеме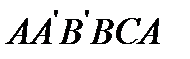 
.
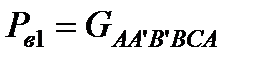Вертикальная составляющая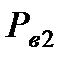 
силы давления жидкости на нижнюю часть поверхности тела направлена вверх и равна весу жидкости в объеме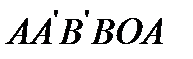 
.
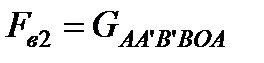Отсюда следует, что вертикальная равнодействующая сил давления жидкости на тело будет направлена вверх и равна весу жидкости в объеме, равном разности указанных двух объемов, т.е.
.
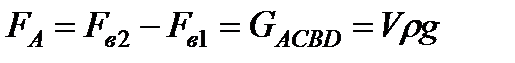В этом и заключается закон Архимеда, обычно формулируемый так: на тело, погруженное в жидкость, действует выталкивающая сила, направленная вертикально вверх, численно равная весу жидкости, вытесненной телом, и приложенная в центре тяжести объема погруженной части тела.
Сила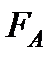 
. называется архимедовой силой, или силой поддержания, а точка ее приложения, т.е. центр тяжести объема 
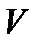- центром водоизмещения.
В зависимости от соотношения веса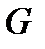 
тела и архимедовой силы 
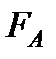возможны три случая:
1) 
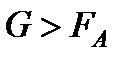- тело тонет;
2) 
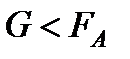- тело всплывает и плавает на поверхности жидкости в частично погруженном состоянии;
3) 
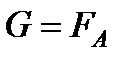- тело плавает в полностью погруженном состоянии.
Для равновесия плавающего тела кроме равенства сил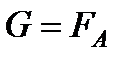 
должен быть равен нулю суммарный момент. Последнее условие соблюдается тогда, когда центр тяжести тела лежит на одной вертикали с центром водоизмещения.
Условие устойчивого равновесия тела, плавающего в полностью погруженном состоянии, заключается в следующем: центр тяжести тела должен находиться ниже центра водоизмещения. Устойчивость равновесия тел, плавающих на поверхности жидкости, здесь не рассматривается.
