С постоянным ускорением

Предположим, что открытый резервуар вместе с находящейся в ней жидкостью движется в вертикальном направлении сверху вниз с некоторым постоянным ускорением 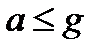, равным или меньшим ускорению свободного падения 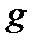(рис. 2.20).

В этом случае на любую точку 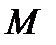в жидкости действуют две единичные массовые силы:

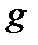- сила тяжести;

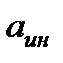- сила инерции переносного движения.

Результирующая массовая сила 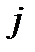, действующая на жидкость, равна сумме векторов силы тяжести и силы инерции, и направлена в сторону, обратную ускорению .

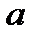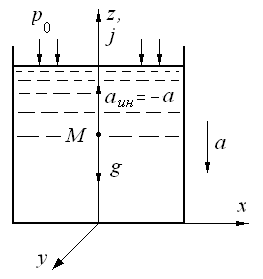
Рис. 2.20. Относительное равновесие жидкости

при движении по вертикали

Обозначив вектор равнодействующей массовой силы, отнесенной к единице массы, через 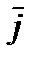получим

,

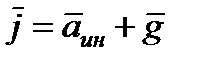где 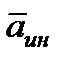и 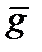- векторы единичных сил инерции и тяжести.

Определим:

1) вид поверхности уровня;

2) закон распределения гидростатического давления.

Заметим, что, согласно принципу Даламбера, при любом движении тела можно пользоваться уравнениями статики, если к системе действующих сил прибавить силы инерции (они направлены в сторону, противоположную направлению движения). Такая система сил будет уравновешена, и тело можно считать находящимся в равновесном состоянии. Воспользуемся дифференциальным уравнением поверхности уровня (2.12)

.

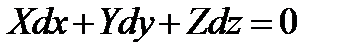Определим для данного случая проекции единичных массовых сил 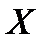, 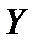и 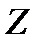, которые численно равны ускорениям. Ускорение свободного падения 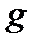(9,81 м/с²) и ускорение сил инерции 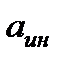направлены параллельно оси 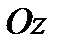. Следовательно, проекции этих ускорений на ос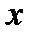и и 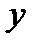равны нулю: 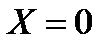и 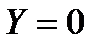. Проекция на ось 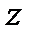равна

.

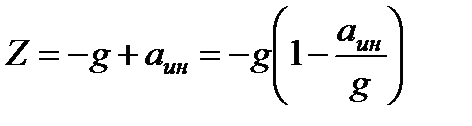Подставив 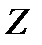в дифференциальное уравнение поверхности, получим

.

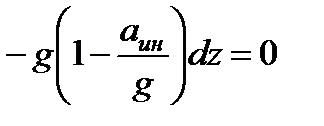Учитывая, что 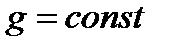, а 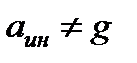, т.е. 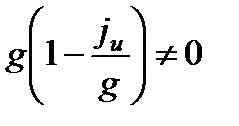, следовательно, для выполнения равенства необходимо, чтобы .

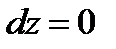Интегрируя последнее выражение, находим 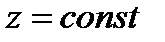. А это значит, что поверхность уровня будет горизонтальной плоскостью.

Если 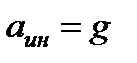, то 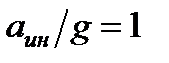и тогда 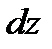может быть и не равным нулю, следовательно, форма свободной поверхности может быть произвольной.

Определим теперь закон распределения гидростатического давления для этого случая. Запишем основное уравнение гидростатики в дифференциальной форме (2.10)

.

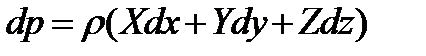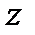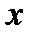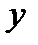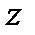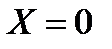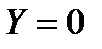Для нашего случая ось направлена вертикально вверх, а оси и лежат в плоскости нормальной оси , поэтому проекции единичных массовых сил будут равны и и .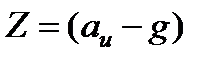

Тогда уравнение гидростатики примет вид

.

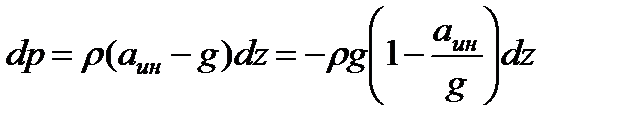Так как 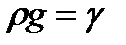, получим

,

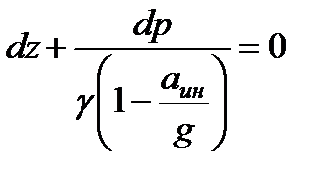Введем обозначение

.

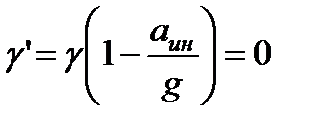где 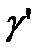представляет собой объемный вес жидкости 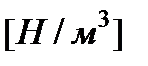в условиях вертикального спуска с ускорением ;

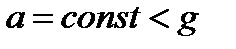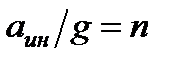- коэффициент перегрузки или просто перегрузка.

Делая подстановку, получим

,

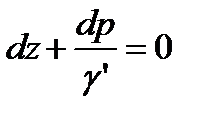и после интегрирования найдем закон распределения давления

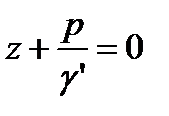. (2.27)

Таким образом, в условиях спуска по вертикали с ускорением 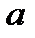закон распределения гидростатического давления будет таким же, как и в обычных условиях равновесия жидкости в поле земного тяготения. Отличие заключается в том, что в подвижной системе координат удельный вес жидкости зависит от коэффициента перегрузки .

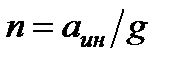Причем, если 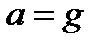, то при свободном падении, объемный вес 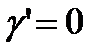, т.е. жидкость стала «невесомой».

Если ускорение 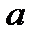имеет знак минус, т.е. происходит торможение, объемный вес 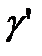будет «тяжелее» в 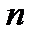раз. Таким образом, вес жидкости при относительном равновесии зависит от коэффициента перегрузки.