2015-06-04
1372
Предположим, что открытый цилиндрический сосуд с жидкостью приведен во вращательное движение вокруг вертикальной оси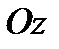 
с угловой скоростью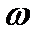 
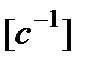(рис. 2.21).
Вращающиеся стенки цилиндра приведут во вращательное движение ближайшие к стенкам слои жидкости, а затем, вследствие вязкости жидкости - и всю ее массу. По истечении известного времени все частицы жидкости будут вращаться примерно с одной и той же угловой скоростью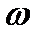 
, а свободная поверхность жидкости видоизменится. В центральной части уровень понизится, а у стенок – повысится. Допустим, что такой момент времени наступил. Определим форму поверхности уровня и, в частности, свободной поверхности.
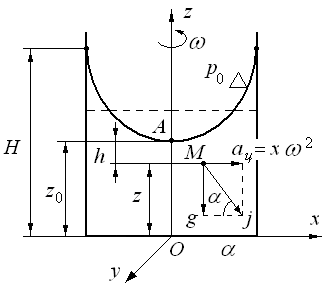
Рис. 2.21. Относительное равновесие при вращении жидкости
вокруг вертикальной оси
Оси координат, как обычно, свяжем с сосудом. При этом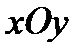 
будет представлять собой горизонтальную плоскость, а ось 
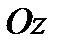- направлена вертикально вверх. Отметим в жидкости произвольную точку 
.
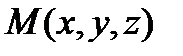Как и в предыдущей задаче, используем общее дифференциальное уравнение поверхности уровня (2.12)
.
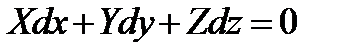Так как движение симметрично относительно оси вращения, то рассмотрим равновесие частиц жидкости, расположенных в плоскости координат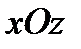 
.
На жидкость действуют единичные объемные силы:
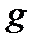- сила земного тяготения; 
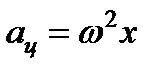-сила инерции.
Сила инерции представляет собой центробежную силу, направленную параллельно оси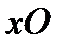 
в сторону от оси вращения.
Следовательно, равнодействующая внешних объемных сил равна
,
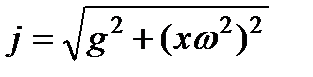и направлена по нормали к свободной поверхности под углом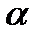 
к оси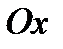 
.
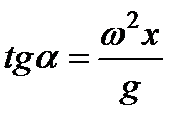Очевидно, что в данном случае проекции единичных массовых сил:
; 
; 
.
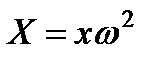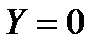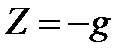Делая подстановку в основное уравнение поверхности, получим:
,
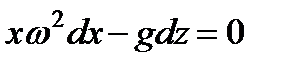или
,
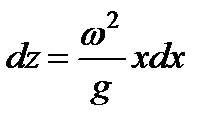и после интегрирования
.
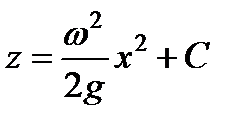Постоянную интегрирования находим при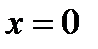 
, 
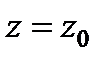, т.е. 
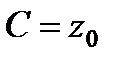. Тогда уравнение поверхности представляет собой параболу с вершиной в точке 
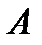на оси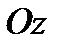 
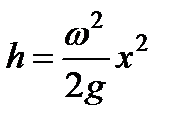, (2.28)
где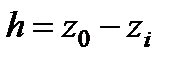 
- глубина погружения точки 
.
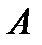Поскольку уравнение симметрично относительно оси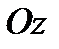 
, постольку поверхность уровня будет представлять собой параболоид вращения.
Закон распределения давления найдем, используя основное дифференциальное уравнение гидростатики (2.10)
.
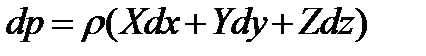Так как проекции единичных массовых сил равны
; 
; 
,
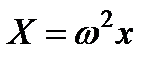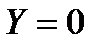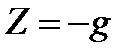то после подстановки, имеем
,
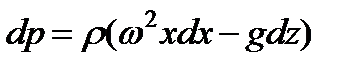или
,
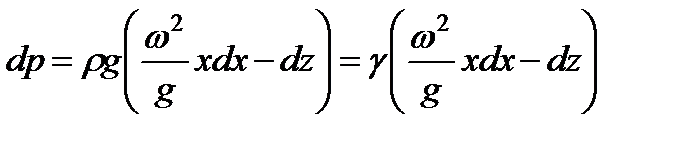или
.
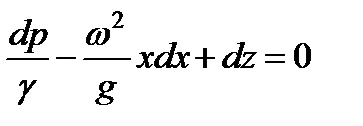Интегрируя, находим (пр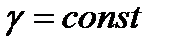и 
и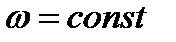 
)
.
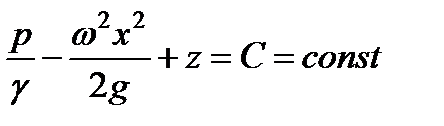Для определения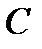 
возьмем точку 
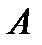на свободной поверхности при 
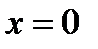. Для этой точки 
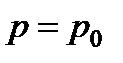(давление атмосферное), 
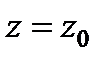(координата вершины параболы).
Тогда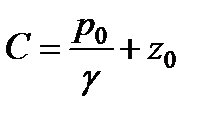 
, и после подстановки
.
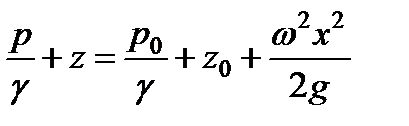Учитывая, что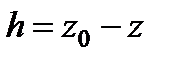 
и умножив обе части на 
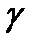, получим значение давления для всех точек любой вертикали на расстоянии 
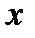от оси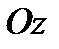 
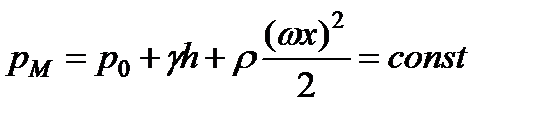. (2.29)
Как видим, при вращении сосуда с жидкостью давление в некоторой точке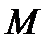 
складывается из трёх частей:
1) внешнего давления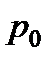 
на свободной поверхности;
2) весового давления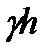 
;
3) давления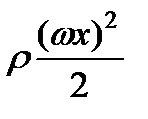 
, производимого центробежной силой.
При этом давление в разных точках одной и той же горизонтальной плоскости не остается здесь постоянным, а изменяется по параболическому закону – пропорционально квадрату текущего радиуса вращения. С другой стороны, при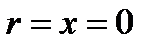 
распределение давления остается таким же, как при «абсолютном» равновесии.
