Изучения движения жидкости (Лагранжа и Эйлера)

Гидродинамика – раздел гидравлики, изучающий законы движения жидкости. Жидкость в гидродинамике рассматривается как сплошная среда, которая состоит из множества частиц, движущихся одна относительно другой.

Главной задачей гидродинамики является определение скоростей (поля скоростей) и гидродинамических давлений в любой точке жидкости. Рассматривая движущуюся жидкость, различают две основные задачи гидродинамики – внешнюю и внутреннюю.

1. Внешняя задача. Заданы характеристики потока. Требуется найти силы, действующие на то или другое тело при обтекании его потоком. Эта задача возникает в машиностроении при проектировании различных насосов и турбин, а в аэродинамике в связи с потребностями авиации (теория крыла, динамика полета) и судостроения.

2. Внутренняя задача. Заданы силы, действующие на жидкость. Требуется определить гидродинамические характеристики потока – скорость, давление и др. Эта задача чаще встречается в технической гидравлике, её мы и будем в основном рассматривать.

В гидравлике движение жидкости рассматривается как движение системы неограниченного множества материальных точек. При этом все частицы жидкости движутся различно, каждая по своей траектории, с различными скоростями и ускорениями. Такое движение представляет собой чрезвычайно сложный процесс, изучение которого связано с большими трудностями.

Целью изучения движения жидкости является определение кинематических характеристик – скоростей и ускорений, а на их основе – динамических характеристик, необходимых для решения практических задач.

Существуют два принципиально отличных метода изучения движения жидкости. Оба метода связаны с именами известных математиков и механиков – Жозефа Луи Лагранжа (1736-1813 г.г.) и Леонарда Эйлера (1707-1783 г.г.).

В обоих методах жидкость (капельная и газообразная) рассматривается как непрерывная среда, сплошь занимающая данное пространство. В качестве мельчайшего элемента жидкости принимается «частица» бесконечно малых размеров, но не отождествляемая с молекулой или атомом.

Метод Лагранжа. Метод Лагранжа основан на исследовании движения отдельных частиц жидкости при их перемещении в пространстве.

В методе Лагранжа положение индивидуальной частицы описывается законом её движения, т.е. тремя уравнениями

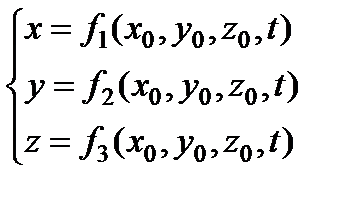; (3.1)

где 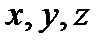- координаты частицы; 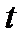- время; 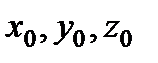- начальные координаты частиц, т.е. положение частиц в начальный момент времени. Следовательно, текущие координаты некоторой движущейся частицы 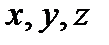являются функциями четырёх переменных 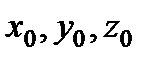и 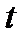. Эти переменные называют переменными Лагранжа.

Совместное решение уравнений (3.1) определяет траекторию MN конкретной частицы с начальными координатами 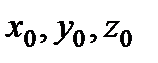в течение времени 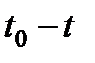(рис. 3.1).

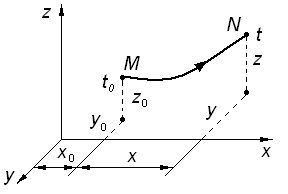
Рис. 3.1. Траектория частицы жидкости

Из теоретической механики известно, что первые производные этих функций по времени определяют компоненты скорости частицы жидкости:

; ; ,

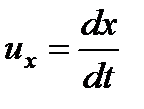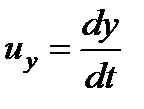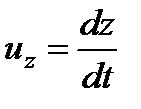а вторые производные – ускорения:

; ; ,

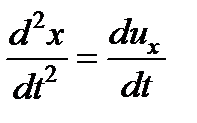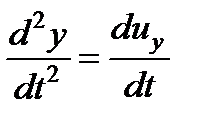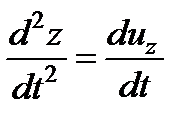где 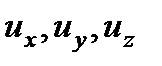- компоненты вектора скорости .

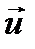Таким образом, в методе Лагранжа исследованию подлежит движение отдельных частиц жидкости.

Метод Эйлера. В методе Эйлера исследуют поля векторных и скалярных параметров движущейся жидкости, не рассматривая вопрос о том, как движется та или иная частица.

При неустановившемся движении каждому моменту времени соответствует своё поле скоростей в рассматриваемой области движения жидкости. Полное описание процесса достигается в том случае, когда определены скорости во всех точках области за весь период наблюдения 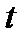. Это можно представить как серию последовательных кадров поля скоростей, полученного киносъёмкой. Если для данной системы координат 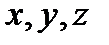определены функции, описывающие изменение поля скоростей и давления во времени

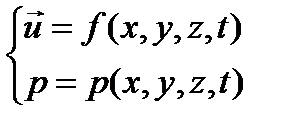то этим решена одна из основных задач гидродинамики – установлен закон распределения скоростей и давлений в потоке.

Таким образом, исследуют поля векторных и скалярных параметров движущейся жидкости, не рассматривая вопрос о том, как движется та или иная частица.

Оба метода исследования жидкости – и метод Лагранжа и метод Эйлера математически связаны между собой и возможен переход от уравнений (3.1) к уравнениям (3.2). Как показало развитие гидравлики, в большинстве случаев метод Лагранжа более сложен и трудоёмок, чем метод Эйлера. Поэтому далее в основном рассматривается решение задач движения жидкости на основе метода Эйлера.

Однако задача отыскания функций скорости и давления методом Эйлера также является весьма сложной. Даже заменяя реальную жидкость моделью «идеальной жидкости», решить её в большинстве случаев не представляется возможным.

Поэтому в технической гидродинамике идут по иному пути и используют так называемый «гидравлический метод». Гидравлический метод (метод технической гидродинамики) основан на использовании некоторых осреднённых и интегральных характеристик потока.

В основу этого метода полагают уравнения, которые существенно отличаются от системы уравнений в методе Эйлера. К числу таких основных уравнений гидравлики относятся следующие:

- уравнение несжимаемости и неразрывности для потока жидкости (уравнение расхода);

- уравнение кинетической энергии для потока реальной жидкости (уравнение Бернулли);

- уравнение количества движения для потока реальной жидкости;

- эмпирические и полуэмпирические зависимости (Дарси и Вейсбаха) для оценки работы сил трения, возникающих в реальной жидкости.

Используя данные уравнения в сочетании с некоторыми приёмами рассмотрения гидравлических явлений (линия тока, средняя скорость и др.) получаем законченную техническую теорию, позволяющую с приемлемой точностью решать большой круг практических задач, относящихся к механике реальной жидкости.