Для потока жидкости

Гидравлика – это техническая механика жидкости, в которой часто используются упрощённые методы для решения инженерных задач. Во многих случаях при решении практических задач гидравлики удобно применять такие центральные понятия механики, как количество движения (уравнение импульсов) и кинетическая энергия.

В связи с этим необходимо рассмотреть возможность вычисления количества движения и кинетическую энергию потока жидкости по средней скорости, а не по действительным местным скоростям. Это позволит существенно упростить гидравлические расчёты.

Для материального тела массой 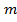, движущегося со скоростью 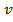, изменение количества движения за время 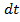вследствие действия силы 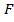выразится векторным уравнением

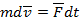, (3.7)

где 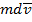- приращение количества движения, обусловленное импульсом .

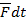Жидкость представляет собой материальную систему, поэтому основной закон механики может быть приложен к любой выделенной из неё массе.

Применим эту теорему механики к участку потока жидкости с расходом 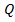между сечениями 1-1 и 2-2 (выделенный участок заштрихован). Ограничимся рассмотрением только установившегося движения жидкости (рис. 3.7).

За время 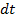этот участок переместится в положение, определяемое сечениям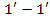и и 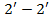. Объёмы этих элементов 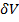, а, следовательно, и их массы 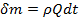одинаковы, поэтому приращение количества движения будет равно

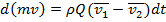. (3.8)

Это приращение количества движения обусловлено импульсом всех внешних сил, действующих на объём жидкости между сечениями 1-1 и 2-2. Внешними силами, приложенными к выделенному объёму, являются сила тяжести всего объёма 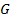, силы давления в первом и втором сечениях 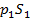и 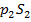(нормальные к этим сечениям и направленные внутрь объёма), а также реакции стенок трубы 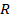, которая складывается из сил давления и трения, распределённых по боковой поверхности объёма.

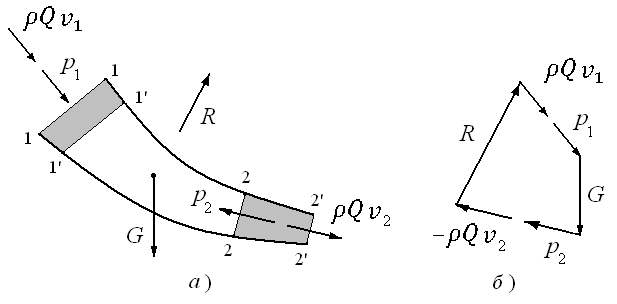
Рис. 3.7. Применение уравнения количества движения

к потоку жидкости

Уравнение импульсов (3.7) для рассматриваемого случая можно записать в виде

.

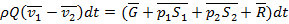После сокращения на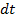

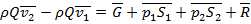. (3.9)

Составив проекции этого векторного уравнения на три координатные оси, получим три алгебраических уравнения с тремя неизвестными - .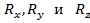

Л. Эйлер предложил удобный графический способ нахождения силы 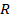. Перенося в формуле (3.?) все слагаемые в одну сторону, можно представить его в виде суммы векторов:

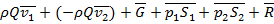= 0, (3.10)

где вектор 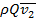взят с обратным знаком (т.е. по направлению обратный действительному). В соответствии с этим выражением (3.10) силу 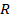можно найти, построив замкнутый многоугольник сил, как это показано на рис. 3.7, а.

Анализ показывает, что при вычислении количества движения и кинетической энергии по средней скорости допускается ошибка, которую можно учесть с помощью двух коэффициентов:

- коэффициента Буссинеска 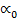при вычислении количества движения ;

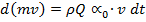- коэффициента Кориолиса 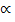в уравнении Бернулли при вычислении кинетической энергии .

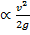Величина обоих коэффициентов зависит от характера распределения скоростей в поперечном сечении потока жидкости. На практике при турбулентном режиме движения коэффициент Кориолиса 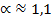, а коэффициент Буссинеска 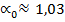. Поэтому обычно полагают 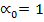. Однако встречаются отдельные случаи, когда 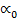достигает больших значений, и тогда пренебрежение им может привести к значительным погрешностям.

Пример 3.2. Определить силу воздействия потока жидкости на преграду. Пусть жидкость вытекает в атмосферу и наталкивается на безграничную стенку, установленную нормально к потоку. В результате жидкость растекается по стенке, изменяя направление своего течения на 90⁰ (рис. 3.8). Известны площадь сечения потока 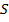, скорость истечения 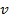и плотность жидкости .

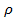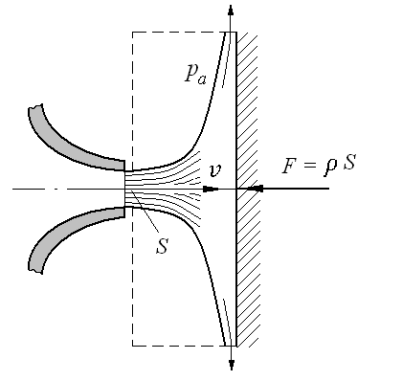
Рис. 3.8. Воздействие струи на преграду

Для решения данной задачи берём фиксированный объём, показанный штриховой линией, и применяем теорему Эйлера. Так как давление внутри струи и по поверхности жидкости равно атмосферному, т.е. избыточное давление равно нулю, уравнение, выражающее теорему Эйлера, для направления, совпадающего с вектором скорости истечения 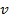, будет иметь вид

,

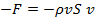или 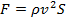. (3.11)

Это и есть сила воздействия потока жидкости на преграду. При другом угле установке стенки или других её форме и размерах в правую формулы (3.11) вводится безразмерный коэффициент, отличный от единицы, но пропорциональность силы 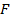произведению 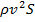сохранится.