Идеальной жидкости в форме уравнений Эйлера

Рассмотрим вопрос о распределении давления в потоке идеальной жидкости. Обратимся к методу, применённому ранее для покоящейся жидкости.

Выделим в потоке жидкости точку А с координатами 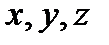в осях, связанных с границами потока (например, со стенками трубопровода (рис. 3.9).

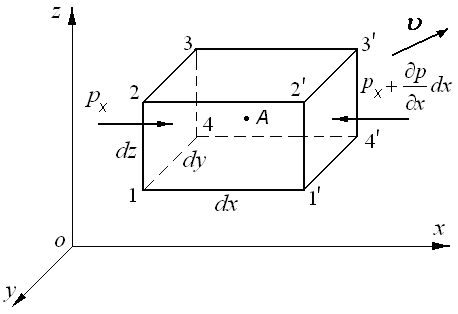
Рис. 3.9. К выводу уравнений Эйлера

Около этой точки выделим элементарный объём жидкости в виде прямоугольного параллелепипеда с боковыми рёбрами 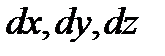, как это было сделано в гидростатике.

На движущуюся жидкость действуют массовые силы – силы тяжести и силы инерции, а также силы давления, действующие на грани и направленные внутрь рассматриваемого объёма.

Пусть давление в этой точке 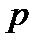, плотность 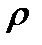. Скорость движения частицы жидкости обозначим через 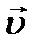, а её проекции на оси - 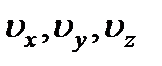. Тогда проекции ускорения, с которым движется выделенный объём, будут равны 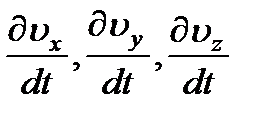. Масса выделенного объёма - 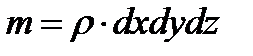. Будем считать, что внутри этого объёма на жидкость действует результирующая массовая сила, единичные проекции которой на оси координат равны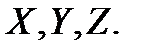

Составим уравнение движения выделенного объёма жидкости. Для этого спроектируем силы, действующие на него, в направлении оси .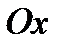

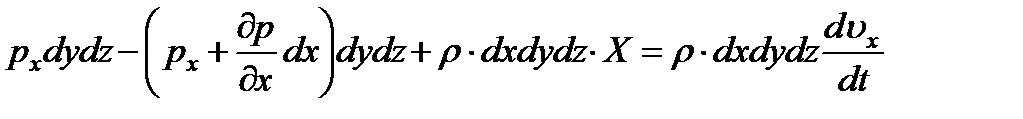. (3.12)

После деления на 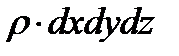и преобразования, получим

.

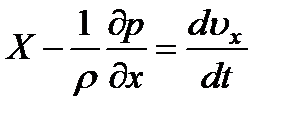Рассматривая аналогичным образом условия равновесия этого объёма относительно 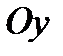и 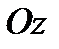, приходим к системе дифференциальных уравнений движения идеальной жидкости Эйлера (3.13).

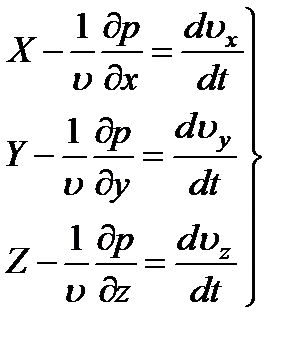(уравнения Эйлера) (3.13)

Эти уравнения аналогичны уравнениям гидростатики, с тем, однако существенным отличием, что они, в соответствии с принципом Даламбера, содержат в правой части производную от соответствующей проекции скорости по времени.

Члены этих уравнений представляют собой ускорения, а физический смысл каждого уравнения состоит в следующем: полное ускорение частицы вдоль координатной оси складывается из ускорений от массовых сил и ускорений от сил давления.

Уравнения Эйлера справедливы как для несжимаемой жидкости, так и сжимаемой. Поскольку при выводе уравнений не накладывались условия стационарности движения, то они справедливы также и для неустановившегося движения.

Эти уравнения, как и уравнения гидростатики, были впервые выведены Леонардом Эйлером в 1755 году.