Основы гидродинамического подобия

В науке существуют два основных метода исследования: аналитический, основанный на законах механики и физики, и экспериментальный.

Ранее отмечалось, что аналитическое решение дифференциальных уравнений, описывающих движение жидкости, возможно лишь для сравнительно небольшого числа упрощенных моделей и явлений. Поэтому для решения большинства сложных инженерных задач в механике жидкости прибегают к экспериментальным исследованиям. Экспериментальные исследования проводятся в лабораториях на моделях, которые выполняются, как правило, в меньшем масштабе, по сравнению с натурными объектами. При этом моделирование изучаемых процессов должно быть научно обосновано.

Исследования на моделях приводят к значительной экономии средств, позволяют уточнять формулы, полученные теоретическим путем, и устанавливать эмпирические зависимости между параметрами изучаемого явления.

В гидравлике множество исследовательских задач позволяет решать теория гидродинамического подобия, т.е. подобия потоков несжимаемой жидкости.

Гидродинамическое подобие складывается из трёх составляющих: геометрического подобия, кинематического и динамического.

1. Геометрическое подобие -представляет собой пропорциональность сходственных размеров и равенство соответствующих углов:

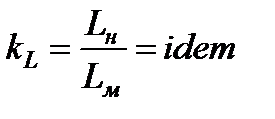, (3.37)

где 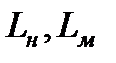- линейные размеры натурного потока и модели;

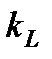- коэффициент пропорциональности или линейный масштаб модели. Эта величина одинакова (idem) для подобных потоков.

В гидравлике под геометрическим подобием понимают подобие тех поверхностей, которые ограничивают потоки, т.е. подобие каналов. К их числу относятся также участки, расположенные непосредственно перед и за рассматриваемым участком, т.к. они оказывают существенное влияние на характер исследуемых явлений.

Из формулы (3.37) следует, что 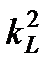является условием подобия соответствующих площадей, а 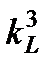- объёмов.

Однако геометрическое подобие является необходимым, но недостаточным условием для адекватного отражения работы натурного объекта и модели.

2. Кинематическое подобие - означает пропорциональность местных скоростей в сходственных точках и равенство углов, характеризующих направление этих скоростей:

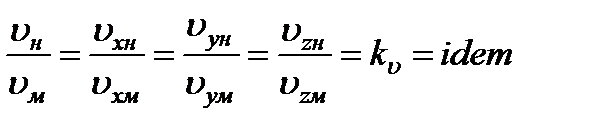, (3.38)

где 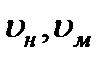- скорость натурного потока и модели;

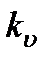— масштаб скоростей, одинаковый при кинематическом подобии.

Так как 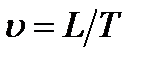, то 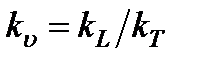(где Т -время, 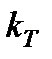- масштаб времени).

Из кинематического подобия потоков следует геометрическое подобие линий тока.

В теории подобия доказывается, что кинематическое подобие потоков (скорости, ускорения, перемещения частиц в модели будут соответственно в одних и тех же отношениях уменьшены по сравнению с натурой) имеет место только при соблюдении геометрического и динамического подобия.

Динамическое подобие - это пропорциональность сил, вызывающих рассматриваемое движение в модели, по сравнению с аналогичными силами в натуре.

В потоках жидкостей обычно действуют разные силы: силы дав­ления, вязкости (трения), тяжести и др. Соблюдение их пропорцио­нальности означает полное гидродинамическое подобие. Осуще­ствление на практике полного гидродинамического подобия оказы­вается весьма затруднительным, поэтому обычно имеют дело с ча­стичным (неполным) подобием, при котором соблюдается пропор­циональность лишь основных, главных сил.

Для напорных течений, т.е. для потоков в трубах, в гидромашинах и тому подобных, такими силами, как показывает анализ, являются силы давления, вязкости и силы инер­ции. На жидкость действует также сила тяжести, но в напорных потоках ее действие проявляется через давление, т.е. оно сводится к соответствующему изменению давления. Поэтому, рассматривая так называемое приведенное давление 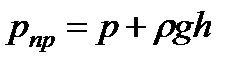, тем самым учитываем силу тяжести.

Силы инерции определяются произведением массы на ускорение, т.е. 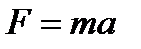, а их отношение в подобных потоках равно масштабу сил:

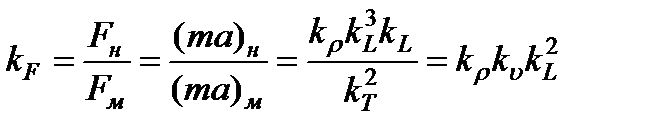, (3.39)

где 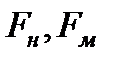- силы инерции в натурном потоке и модели;

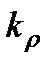- масштаб плотностей.

Таким образом, силы инерции пропорциональны плотности, ско­рости во второй степени и размеру L во второй степени, который, в свою очередь, пропорционален площади S:

.

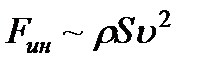Заметим, что этому же произведению 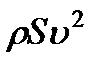пропорциональны силы, с которыми поток воздействует (или способен воздействовать) на преграды (см. п. 3.6), лопасти гидромашин и обтекаемые тела.

Примем силы инерции за основу и будем другие силы, действую­щие на жидкость, сравнивать с инерционными, т.е. с выражением .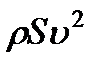

Таким образом, для гидродинамически подобных потоков в натуре (н) и модели (м) имеем

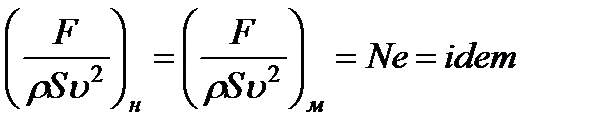(число Ньютона). (3.40)

Это отношение, одинаковое для подобных потоков, называют числом Ньютона и обозначают 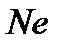. Здесь под 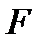подразумевается основная сила: сила давления, вязкости, тяжести или др. Следова­тельно, соотношение (3.40) представляет собой общий вид закона гидродинамического подобия.

Рассмотрим три характерных случая воздействия на движущуюся жидкость основных сил и найдем усло­вия подобия потоков.

1. На жидкость действуют лишь силы давления и инерции. Тогда 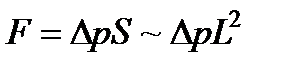и условие (3.40) примет вид

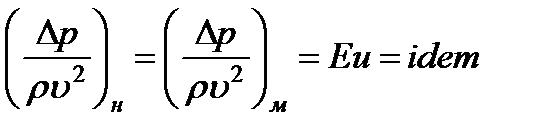(число Эйлера), (3.41)

где 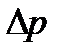- некоторая разность давлений (или просто давление);

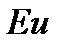- безраз­мерный критерий, называемый числом Эйлера.

Следовательно, условием гидродинамического подобия геомет­рически подобных потоков в данном случае является равенство для них чисел Эйлера.

Из предыдущего ясен физический смысл числа Эйлера: это есть величина, пропорциональная отношению сил давления к силам инерции.

2. На жидкость действуют силы вязкости, давления и инерции. Тогда

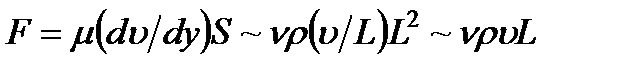
и условие (3.40) после деления последнего выражения на 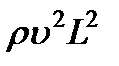при­мет вид

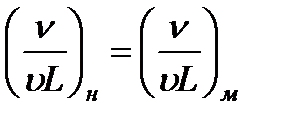, или

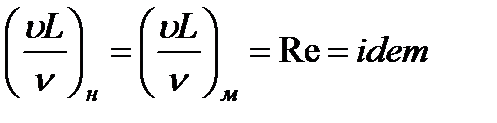(число Рейнольдса), (3.42)

где Re — безразмерный критерий, называемый числом Рейнольдса.

Отступление. 0. Рейнольдс (1842—1912 гг.) - известный английский физик и инженер. Помимо установления важнейшего критерия, названного его именем, исследовал ряд других вопросов гидравлики с позиций инженера: режимы те­чения жидкости, теорию наиболее сложного турбулентного режима течения, теорию смазки, течение с парообразованием (кавитацию) и др.

Следовательно, условием гидродинамического подобия геомет­рически подобных потоков в рассматриваемом случае является ра­венство чисел Рейнольдса, подсчитанных для сходственных сечений потоков.

Последнее условие является особенно важным, так как им устанавливается основной критерий подобия напорных потоков - число Рейнольдса. За характерный размер L при под­счете числа Рейнольдса должен приниматься поперечный размер потока, например, диаметр сечения.

Из предыдущего ясен физический смысл числа Рейнольдса: это есть величина, пропорциональная отношению сил вязкости к силам инерции.

3. На жидкость действуют силы тяжести, давления и инерции. Тогда 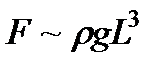и условие (3.40) принимает вид

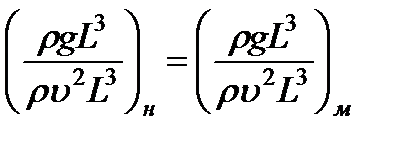или

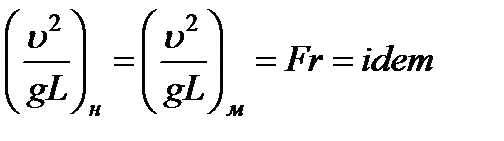(число Фруда), (3.43)

где 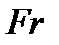- безразмерный критерий, называемый числом Фруда.

Следовательно, условием гидродинамического подобия геометри­чески подобных потоков в данном случае является равенство чисел Фруда. Из предыдущего яс­но, что число Фруда — это величина, пропорциональная отношению сил инерции к силам тяжести. Критерий Фруда являет­ся важным при рассмотре­нии безнапорных течений в открытых руслах, для на­порных течений его можно не учитывать.

Для установления связи между гидродинамическим подобием и основным уравнением гидравлики - уравнением Бернулли - рассмотрим два напорных потока I и II, которые подобны друг другу гидродинамически, и отметим на них сходственные сечения 1-1 и 2-2 (рис. 3.17).

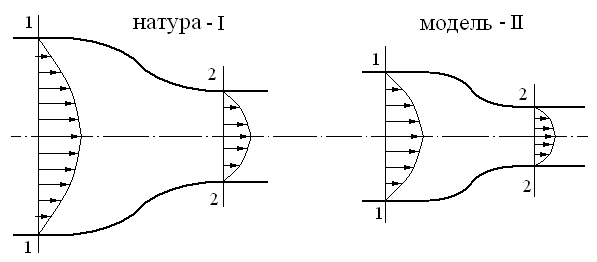
Рис. 3.17. Подобные потоки

Запишем уравнение Бернулли для указанных сечений одного из потоков в предположении, что жидкость идеальная. Это будет соответствовать первому из рассмотренных выше случаев движения, так как на жидкость, можно считать, будут действовать лишь силы давления и инерции. Будем иметь

,

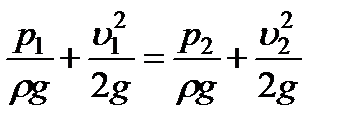где 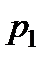и 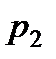— приведенные давления.

Используя уравнение расхода

,

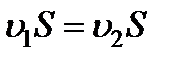исключим скорость 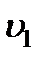и, перегруппировав члены уравнения, приведем его к безразмер­ному виду. Для этого разделим уравнение на 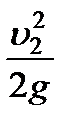, после чего получим

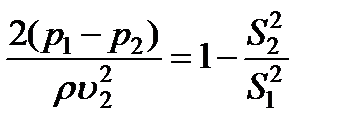. (3.44)

Правая часть уравнения (3.44) одинакова для подобных пото­ков вследствие геометрического подобия, а левая часть, представ­ляющая собой удвоенное число Эйлера 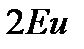, одинакова вследствие динамического подобия, и всё уравнение (3.44) одинаково для по­добных потоков идеальной жидкости. Таким образом, для обеспе­чения гидродинамического подобия напорных потоков идеальной жидкости достаточно одного геометрического подобия.

Теперь запишем уравнение Бернулли для тех же сечений 1-1 и 2-2 одного из напорных потоков вязкой жидкости, подобных гидродинамически. Будем иметь

,

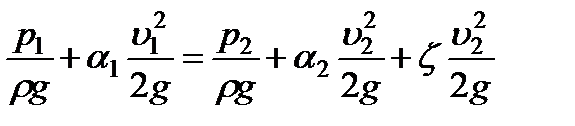где 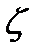- коэффициент потерь энергии между рассматриваемыми сечениями.

После приведения этого уравнения к безразмерному виду подобно предыдущему получим

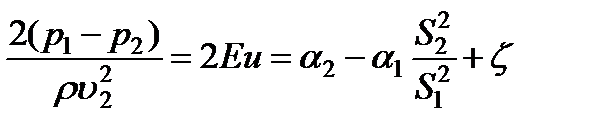. (3.45)

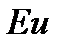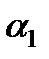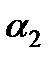Число одинаково для рассматриваемых подобных потоков вследствие их динамического подобия; коэффициенты Кориолиса и одинаковы из-за кинематического подобия, следовательно, одинаковым будет и коэффициент потерь 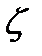, а также все уравнение.

Если же рассматривать подобные потоки в трубах постоянного сечения, то одинаковым будет коэффициент потерь на трение по длине - .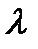

Итак, в подобных напорных потоках имеем равенство безразмер­ных коэффициентов и чисел 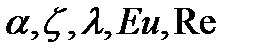и некоторых других, которые будут введены в рассмотрение ниже.

Изменение числа 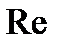означает, что изменяется соотношение основных сил в потоке, в связи с чем указанные коэффициенты могут также несколько изме­ниться. Поэтому все коэффициенты следует рассматривать как функ­ции основного и определяющего критерия для напорных потоков вязкой жидкости — числа Рейнольдса - 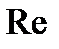(хотя в некоторых интер­валах числа 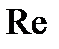эти коэффициенты могут оставаться постоянными).

При экспериментальных исследованиях и моделировании напор­ных течений в лабораторных условиях необходимо, во-первых, обес­печить геометрическое подобие модели (II) и натуры (I), включая условия входа и выхода, и, во-вторых, соблюсти равенство чисел Рейнольдса: 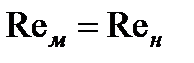. Из второго условия получаем необходимую скорость потока при эксперименте

.

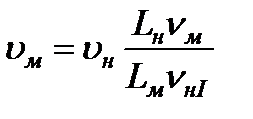В частном случае, при 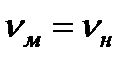скорость при эксперименте должна быть больше натурной в 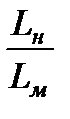раз. Применяя менее вязкую жид­кость (или ту же жидкость, но при повышенной температуре) можно снизить скорость .

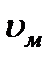Помимо перечисленных основных критериев подобия (Eu, Re, Fr), в гидравлике применяют и другие критерии для особых случаев течения жидкости. Так, при рассмотрении течений, связанных с по­верхностным натяжением (например, при распаде струи на капли, распыливании топлива в двигателях), вводят критерий Вебера (We), равный отношению сил поверхностного натяжения к силам инерции. Для этого случая условие (3.40) принимает вид

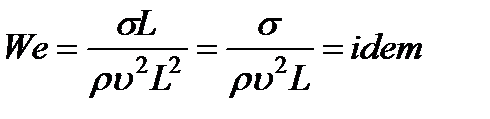(критерий Вебера). (3.46)

При рассмотрении неустановившихся (нестационарных) периодических течений с периодом 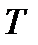(например, течений в трубопроводе, присоединенном к поршневому насосу) вводят критерий Струхаля (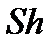), учитывающий силы инерции от нестационарности, называемые локальными. Последние пропорциональны массе (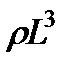)и ускорению 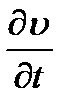, которое, в свою очередь, пропорционально 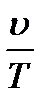. Следовательно, условие (3.40) для этого случая принимает вид

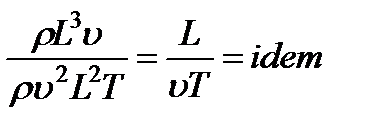или

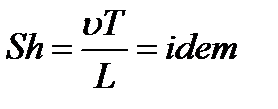(критерий Струхаля). (3.47)

При рассмотрении движений жидкости с учетом ее сжимаемости (например, движений эмульсий) вводят критерий Маха (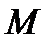), учиты­вающий силы упругости. Последние пропорциональны площади (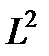)и объемному модулю упругости 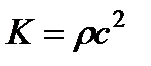[см. сжимаемость – закон Гука]. Поэтому силы упругости пропорциональны 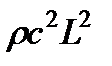и условие (3.40) принимает вид

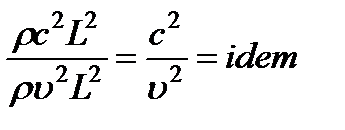или

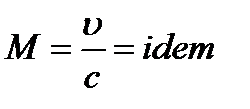(число Маха). (3.48)

Критерий Маха имеет очень большое значение при рассмотрении движений газа. Чем ближе число М к единице, тем больше влияние сжимаемости газа при его движении.