Задача № 3

	Доля расходов на покупку товаров и услуг в общей структуре потребительских расходов (Y)	месяц х1	Среднемесячный душевой доход - Х1	Среднемесячная номинальная ЗП-Х2 тыс.руб	Индекс потребительских цен, % - X3
	82,7			18,4	106,4
	73,7		11,3
			11,9	13,3	105,1
	80,7		20,2		105,9
	71,3		14,5	15,8	106,7
	75,1		12,1	14,9	106,2
	74,2		21,3	18,8	106,7
			14,7	14,6	106,7
	75,4		18,3	18,5	106,7
	71,7		14,9		105,7
	72,4		14,2	16,4	105,6
	73,2		21,8	18,6	105,7
	73,7		13,1	16,2	105,3
	70,2		14,3		106,7
сумма	1024,3		221,6	231,5	1485,4
среднее	73,1642857	7,5	15,82857	16,53571	106,1

1) Расчитаем параметры модели:

a0
a1=		11,3	11,9	20,2	14,5	12,1	21,3	14,7	18,3	14,9	14,2	21,8	13,1	14,3
a2			105,1	105,9	106,7	106,2	106,7	106,7	106,7	105,7	105,6	105,7	105,3	106,7

	18,4	106,4
	13,3	105,1
		105,9
	15,8	106,7
	14,9	106,2
	18,8	106,7
	14,6	106,7
	18,5	106,7
		105,7
	16,4	105,6
	18,6	105,7
	16,2	105,3
		106,7

82,7
73,7
80,7
71,3
75,1
74,2
75,4
71,7
72,4
73,2
73,7
70,2

		231,5	1485,4
(Х/Х)=	221,6	3751,45	23519,2
	1485,4	24564,68	157605,1

	2807,17167	0,580934	-26,5438
(Х/Х)-1=	2,10537815	0,012105	-0,02165
	-26,785242	-0,00736	0,253551

	1024,3
(Х/Y)=	16338,79
	108688,98

	-139,22528
A=(Х/Х)-1×(Х/Y)=	1,28746105
	1,80113547

2) Уравнение регрессии зависимости доли расходов на покупку товаров и услуг (в общей структуре потребительских расходов) от среднемесячного душевого дохода

Y=-139,225+1,29Х+1,80X²

3) Оценим качество модели:

R=0,55

R²=R_{у,x1, х2}=0,3025

Коэффициент детерминации показывает 30,2% вариаций.

4) Оценим значимость уравнения регрессии на основе критерия Фишера:

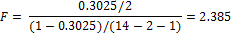
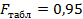
Так как 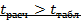, то уравнение регрессии следует признать значимым, тоесть его можно использовать для анализа и прогноза

5) Оценим с помощью t-критерия Стьюдента статистическую значимость коэффициентов:

	2807,17167	0,580934	-26,5438
(Х/Х)-1=	2,10537815	0,012105	-0,02165
	-26,785242	-0,00736	0,253551

b₁₁=2807,17167

b₂₂=0,012105

b₃₃=0,253551

t_a0= -139,225/( 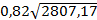)=3,20

t_a1= 1,29/( 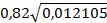)=14,30

t_a2= 1,80/( 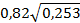)=4,36

Так как 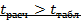, то коэффициенты а₁, а₂ следует признать значимым.

6) Для каждого коэффициента регрессии вводим коэффициент эластичности и β- коэффициент:

Э_j=a_jx_j/y

Э₁=1,29*15,83/73,16=0,28

Э₂=1,8*106,1/73,16=2,61

β_j=a_jSx_j/Sy

β₁=1,29* 0,57 /5,10=0,144

β₂=1,29* 3,58 /5,10=0,905

Доля расходов на покупку товаров и услуг в общей структуре потребительских расходов 0,144*5,10=0,735

Коэффициент эластичности Э₁показывае, что при увеличении среднемесячного душевого дохода на 1% доля расходов на покупку товаров и услуг в (общей структуре потребительских расходов) увеличивается на 0,28%.А коэффициент β₁ показывает что при увеличении среднемесячной номинальнойзароботной платы на 0,14%доля расходов на покупку товаров и услуг в (общей структуре потребительских расходов) увеличивается на 0,735 тыс.руб..

7) Определим точечные и интервальные оценки доли расходов на покупку товаров и услуг в (общей структуре потребительских расходов)

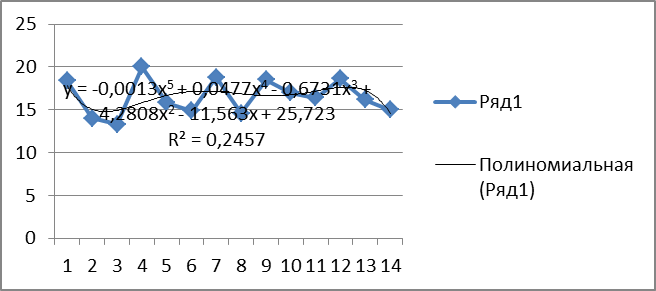
Для фактора Х₁ «Среднемесячный душевой доход» выбрана модель:

Х₁₌25,72-11,56t+4.28t²-0,673t³+0.047t⁴

Y=-0,006х⁵+0,047х⁴-0,673t³+4,319х²-11,616х+12,831

Для временного ряда «Индекс потребительских цен» в качестве аппроксимирующей функции полином второй степени:

Х2=105,8+0,109t – 0,007t²