Предположим, что результаты наблюдения 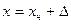 некоторой физической величины
некоторой физической величины 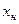 содержат только случайную погрешность ∆
содержат только случайную погрешность ∆ 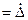 . Данные результаты, как и случайная погрешность ∆, являются случайной величиной.
. Данные результаты, как и случайная погрешность ∆, являются случайной величиной.
Свойства случайной величины х наиболее полно описывается законом распределения 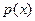 , соответствующим закону распределения ее случайной погрешности ∆.
, соответствующим закону распределения ее случайной погрешности ∆.
Примеры нормального и равномерного законов распределения 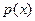 показаны ниже
показаны ниже
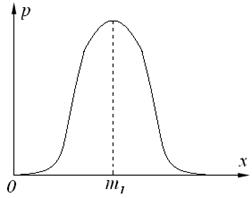
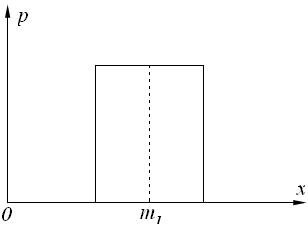
а) б)
Законы распределения случайной величины:
А – нормальный; б) – равномерный,
m1 – центр распределения случайной величины.
Аналитическое представление данных законов получается путем преобразования координат в ранее приведенных формулах, т.е переходом к новой переменной х.
Нормальный закон распределения случайной величины х описывается выражением:
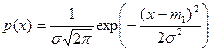 ,
,
где 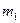 и
и 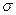 - соответственно математическое ожидание и СКО случайной величины.
- соответственно математическое ожидание и СКО случайной величины.
Вероятность 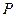 попадания величины х в некоторый интервал (х1, х2) вычисляется по формуле:
попадания величины х в некоторый интервал (х1, х2) вычисляется по формуле:
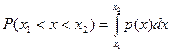 .
.
Для описания отдельных свойств случайной величины х используются числовые характеристики законов распределения р(х) – начальные и центральные моменты k -го порядка, представляющие собой некоторые средние значения. Моменты называются начальными, если с их помощью усредняются величины, отсчитываемые от начала координат, и центральными, если усредняются величины, отсчитываемые от центра распределения.
|
|
|
Начальный момент первого порядка (математическое ожидание случайной величины) определяет центр распределения р(х) и описывается выражением
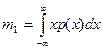
Центральный момент второго порядка (дисперсия случайной величины) характеризует рассеяние значений случайной величины и вычисляется как
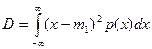 .
.
 2015-06-14
2015-06-14 667
667








