2015-06-14
795
Рассмотренные функции распределения р(х) описывают поведение непрерывных случайных величин х, возможные значения которых неотделимы друг от друга и непрерывно заполняют некоторый конечный или бесконечный интервал. Поэтому выражения моментов относятся именно к непрерывным величинам. Однако реальное число п наблюдений физической величины хи всегда ограниченно, и поэтому как результаты наблюдений, так и случайные погрешности допустимо считать величинами дискретными, возможные значения которых отделимы друг от друга и поддаются счету. В связи с этим рассмотрим вопрос оценки математического ожидания и СКО для ограниченной группы (выборки) наблюдений, обозначая их через хi (см. распределение Стьюдента).
Такие оценки в метрологии называются точечными и их принято обозначать волнистой чертой, т.е. обозначать через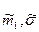 
и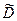 
. Сразу отметим, что величину 
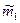, обозначаемую далее 
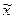, принимают за величину измерения величины хи.
Результат измерений 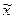= 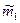при распределении наблюдений по нормальному закону определяют, учитывая закон больших чисел: при достаточно большом числе п независимых наблюдений хi среднее арифметическое полученных значений случайной величины приближается к ее математическому ожиданию 
:
.
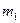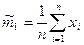Соответственно, при поиске оценки СКО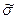 
используют выражение для СКО σ, справедливое для достаточно больших п:
.
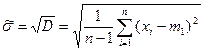Точечные оценки получают по этим формулам при конечном и относительно малом числе наблюдений. Чем число наблюдений больше, тем ближе точечные оценки к величинам 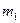и σ.
