Общие положения. Институт управления и территориального развития

К(П)ФУ

Институт управления и территориального развития

Тема 3

Методическая разработка

для выполнения котрольного задания №3

по регрессионному анализу

(дисциплина «Статистика»)

Составитель: к.э.н. Шихалёв А.М.

Казань - 2011

РЕГРЕССИОННЫЙ АНАЛИЗ

Общие положения

Изучение корреляционных зависимостей основывается на исследовании таких связей между переменными, при которых значения одной переменной, которая принимается исследователем за зависимую переменную «в среднем» изменяются в зависимости от того, какие значения принимает другая переменная (признак-фактор), рассматриваемая как причина по отношению к зависимой переменной.

Следовательно, первой и основной задачей регрессионного анализа является определение типа функции, с помощью которой характеризуется зависимость между признаками. Причем теоретическая линия регрессии должна расположиться относительно эмпирической, как правило, ломаной кривой, построенной на точках корреляционного поля так, чтобы сумма отклонений точек поля корреляции от соответствующих точек теоретической линии равнялась нулю, а сумма квадратов этих отклонений была бы минимальной величиной.

Таким образом, методологический аппарат регрессионного анализа так или иначе связан с анализом функций на экстремум. Рассмотрим пример из школьного курса (или из курса математического анализа) анализ функции вида y=f(x), где традиционно х принимается нами в качестве известной величины, y – неизвестной, а вид функции считается известным.

Пример анализа функции на экстремум рассмотрим для наиболее наглядной для такого случая функции – параболической. Перед нами в данном случае стоят две задачи: определить аналитическим путем, есть ли у функции экстремум (максимум или минимум); определить, что же именно – максимум или минимум. Пусть вид функции представлен так (1) В общем виде, где а = 1, а b = 3:

y = f(x) = a + (x - b)² = 1 + (x - 3)². (1)

Для лучшей наглядности визуализируем содержание (1), для чего последовательно зададимся некоторыми значениями х, по формуле (1) найдем соответствующие значения y и занесем их в рабочую таблицу 1.

Таблица 1

Рабочая таблица

№	Х	Y
	1,0 2,0 3,0 4,0 5,0	5,0 2,0 1,0 2,0 5,0

Данные табл. 1 представим графически на рис. 1.

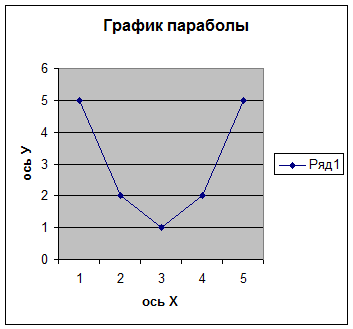Рис. 1. График функции, исследуемой на экстремум

Из рис. 1 видно, что, во-первых, экстремальное значение функции наблюдается при х=3 и что значение функции при этом – минимальное, то есть у=1. При всех остальных значениях х значения функции у будут больше, чем 1.

А теперь сделаем то же самое аналитически. Для этого формулу (1) необходимо продифференцировать, иначе говоря, найти первую производную по х

y_х^Œ = [1 + (x – 3)²] _х^Œ

dy d d

— = — [1 + (x – 3)²] = 0 + 2 (x - 3) ² — (x – 3) = 2 (x – 3) = 2x – 6 (2)

dx dx dx

Для того, чтобы установить, является ли функция экстремальной, полученное выражение (2) достаточно приравнять к нулю:

2х – 6 = 0 (3)

В формуле (3) имеем одно уравнение, линейное по отношению к аргументу х и одно неизвестное. Из (3) находим х = 3 (что видно и из содержания табл. 1). Подставляя х = 1 в выражение (1), получим: у = 1.

Далее следует установить, является ли значение у = 1 для функции (1) максимальным или минимальным по известному правилу: если вторая производная от выражение (2) будет отрицательным, то функция (1) достигает в точке х = 3 свое максимальное значение; если же положительным, то функция (1) достигает в той же экстремальной точке минимальное значение.

d

— (2x – 6) = 2 > 0 (4)

dx

Из выражения (4) видно, что функция у при значении х = 3 достигает своего минимального значения.

Следовательно, располагая только лишь видом функции, даже не визуализируя ее, можно определить ее экстремальное значение и установить его характер (рассмотрение возможного вопроса о единственности экстремума выходит за рамки данного рассмотрения). Важно, что здесь мы рассматриваем переменную х в качестве аргумента, значения коэффициентов а и b и их взаимосвязь полагаем известными. Задаваясь значениями х, получаем значения функции у.

Однако часто в статистике бывает наоборот: х и у известны, но неизвестны значения коэффициентов а и b.

Решением задач в такой постановке и занимается регрессионный анализ. Если переменных всего две, одна из которых подразумевается аргументом, а другая – функцией, что определяется на этапе предшествующего вычислениям в рамках так называемого концептуального (неформализованного) анализа, то аппарат определения неизвестных коэффициентов носит названия парной регрессии или задачей аппроксимации. Если аргументов более одного, то подобная задача решается в терминах множественной регрессии.

Рассмотрим механизм парной регрессии, широко используемый в социально-экономических исследованиях.