Сущность метода наименьших квадратов

Снова запишем вид соотношения (5) и распишем его подробнее:

_{N N N}

S = S (y_i – ŷ_i)² = S [y_i – (a + bx_i) ]² = S (y_i – a - bx_i)² ® min. (7)

^{I=1 I=1 I=1}

Далее потупим так, как и в случае с вышеприведенным примером по нахождению экстремума у функции вида (1), с тем лишь отличием, что в качестве неизвестных переменных будем рассматривать не функцию у, а коэффициенты уравнения (5) а и b. С целью упрощения последующих записей переменные у знака суммы и остальные индексы обозначать не будем.

Для решения поставленной задачи продифференцируем выражение (7) по двум неизвестным а и b в так называемых частных производных.

∂S

— = 2 S (y – a - bx) (0 – 1 - 0) = 2 S (y – a - bx) (-1) = 0. (8)

∂a

Разделим обе части равенства (8) на (-1), в правой части равенства (8) останется 0. Понятно, 2 ≠ 0, следовательно,

S (y – a - bx) = 0. (9)

Распишем выражение (9) следующим образом.

S (y – a - bx) = Sу - Sа - Sb = 0; Sу = Sа + b Sх = а S + b Sх.

Поскольку S = S1= (1 + 1 + … + 1) = N, то выражение (9) примет вид:

S у = аN + b Sх (10)

В уравнении (10) все переменные, то есть Sу, Sх и N, – известные величины, суть исходные данные для получения уравнения регрессии, коэффициент а – неизвестная величина.

Проделаем подобные операции по отношению к еще одной неизвестной величине – коэффициенту b.

∂S

— = 2 S (y – a - bx) (0 – 0 – x) = 2 S (y – a - bx) (-x) = 0. (11)

∂b

Если в выражении (11) 2 ≠ 0, то остальная часть равенства (11) примет вид:

S (yx – ax – bx²) = Syx - Sax - S bx² = 0;

Sxy = a Sx + b Sx² (12)

Таким образом, выражение (8) и (12) составляют систему двух уравнений (13) с двумя неизвестными, коэффициентами а и b, а это, в свою очередь, означает, что данная система уравнений – имеет единственное решение.

æ а N + b Sх = Sу

{ (13)

è a Sx + b Sx² = Sxy

Решение системы уравнений (13) может быть осуществлено несколькими способами: методом подстановки, когда одно неизвестное выражается через другое, методом Крамера (метод определителей) и матричным методом. Заметим, однако, что применение первых двух способов оправдано лишь в случаях, когда число неизвестных не превышает трех. Матричный метод – наиболее универсальный, и именно он используется в вычислительных процедурах на ЭВМ средствами ППП, что рассмотрим несколько ниже.

Для решения системы уравнений (13) воспользуемся методом определителей, как наиболее наглядным, для чего перепишем систему (13) в следующем виде.

(для а) (для b) (для правых частей выражения 13)

| N Sх | | Sу |

| | = | | (14)

| Sх Sx² | | Sxy |

Вычислим главный и частные определители по известным правилам, когда столбцы при соответствующих неизвестных замещаются правыми частями выражения (14):

∆ = N Sx² - (Sх)²,

∆ _a = Sу Sx² - Sх Sxy,

∆ _b = N Sxy - Sх Sу.

Тогда искомые значения коэффициентов а и b будут следующими:

∆ _a Sу Sx² - Sх Sxy

а = — = ———————, (15)

∆ N Sx² - (Sх)²

∆ _b N Sxy - Sх Sу

b = — = ———————, (16)

∆ N Sx² - (Sх)²

Если коэффициенты регрессии а и b вычислены правильно, то в этом легко убедиться по тождеству (16а), иллюстрирующего тот факт, что если мы подставим среднее значение х, то при найденных коэффициентах получим среднее значение у:

у_ср ≡ а + b х_ср. (16а)

Далее рассмотрим процесс нахождения величин коэффициентов линейной функции вида (6) на конкретном, т.н. «модельном» примере.

Пример. В качестве примера обратимся к следующим исходным данным. Пусть некая фирма в текущем году с января по июнь располагает следующими данными по ежемесячной прибыли: в январе, феврале и марте – по 1 тыс.руб.; в апреле – 3 тыс.руб.; в мае – 4 тыс.руб. Требуется построить прогноз ожидаемой прибыли на июнь и оценить ее достоверность – при прочих равных условиях. Под равными условиями этим имеется в виду неизменность (постоянство) внутренних и внешних условий деятельности фирмы (структура производства, позиционирование продукции, коньюнктура, уровень инфляции и др.).

Введем обозначения. Поскольку мы имеем дело с моментным временным рядом, представим месяцы как варианты вариационного ряда – элементы множества Х = {x_i}, где x_i – месяцы текущего года, i=1,n; n=5. То есть x₁= 1 (первый месяц), x₂= 2, x₃= 3, x₄= 4, x₅= 5 (пятый месяц). Тогда прибыль У = {y_i}, где y_i - ежемесячная прибыль в тыс.руб.

Исходные (эмпирические) данные в принятых нами обозначениях представим в виде рабочей таблицы (табл. 2). Причем в табл. 2 предусмотрим такие столбцы, наличие которых позволило бы вычислить все элементы формул (15) и (16).

Таблица 2

Эмпирические данные и промежуточные вычисления

i	xi	yi	xi yi	xi2	yi2
Si = N = 5	Sxi = 15	Syi = 10	Sxi yi = 38	Sxi2 = 55	Syi2 = 28

Опуская для большей наглядности индексы и подставляя данные табл. 2 в выражения (15) и (16), получим следующее.

Sу Sx² - Sх Sxy 10•55 - 15•38 550 – 570 - 20

а = ——————— = —————— = ———— = —— = - 0,4; (17)

N Sx² - (Sх)² 5•55 - (15)² 275 - 225 50

N Sxy - Sх Sу 5•38 - 15•10 190 – 150 40

b = ——————— = —————— = ———— = —— = + 0,8. (18)

N Sx² - (Sх)² 5•55 - (15)² 275 - 225 50

Коэффициенты найдены, и символьное выражение (6) примет явный вид:

ŷ = - 0,4 + 0,8 • х.. (19)

Осуществим проверку корректности вычисления коэффициентов уравнения линейной регрессии по выражению (16а). Тождество (16а) выполняется:

2 ≡ - 0,4 + 0,8 • 3 = - 0,4 + 2,4 = 2

Следовательно, коэффициенты а и b найдены верно.

Выражение (19) относится ко всем действительным значениям х. Однако для нас представляет интерес именно его вещественные значения - дискретные положительные значения – 1, 2, 3 и т.д., - в частности нас интересует прибыль в 6-м месяце текущего года (в июне). Поэтому перепишем (19) с учетом ранее опущенных индексов:

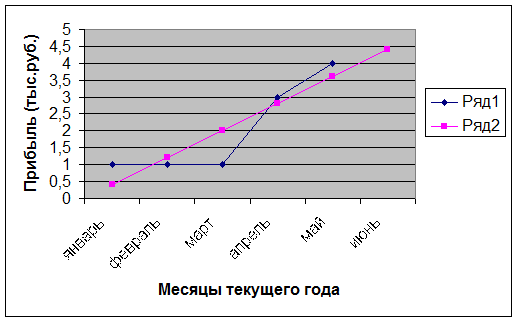
Рис. 2. Эмпирические данные, линия регрессии и прогноз.

ŷ_i = - 0,4 + 0,8х_i. (20)

Для нахождения прогнозного значения прибыли достаточно в выражение (20) подставить х₆=6:

ŷ_i = - 0,4 + 0,8х_i = - 0,4 + 0,8•6 = -0,4 + 4,8 = 4,4 (тыс.руб.). (21)

Эмпирические данные (Ряд 1), линия регрессии и прогноз на следующий месяц (Ряд 2) приведены на рис. 1.

Вполне очевидно, что в общем случае прогноз тем точнее, чем период ретроспекции (здесь - январь-май, то есть 5 месяцев) больше прогнозируемого периода (здесь - июнь, то есть 1 месяц). Иными словами, картину, полученную в виде (19) или (20), мы экстраполируем за пределы проведенной нами аппроксимации – представления некоторой эмпирической зависимости (2 и 3 столбцы табл. 1) в виде некоторой аналитической функции (19), в данном случае – линейной.

Заметим также, что с января по май в одноименных точках по оси абцисс ОХ сумма квадратов разностей эмпирических значений прибыли У (Ряд 1) и их аналитических значений по выражению (20) (Ряд 2) будет минимальной в рамках любой другой линейной функции, то есть функции со значениями коэффициентов а и b, отличных от найденных (а≠-0,4; b≠0,8), что и составляет сущность метода наименьших квадратов (МНК), символически записанной в выражении (5).

Y Y

y = a + bx y = a - bx

0 X 0 X

Рис. 3 Рис. 4

Y Y

y = -a + bx y = a

0 X 0 X

Рис. 5 Рис. 6

Во всех приведенных случаях значение коэффициент «а» со своим знаком иллюстрируется величиной ординаты, отсекаемой прямой от оси ОY. Значение коэффициента «b» есть не что иное, как величина тангенса угла наклона прямой к оси ОХ (отношение длины катета, противолежащего углу, к длине катета, прилежащего к углу). Особенно это наглядно можно проиллюстрировать на примере уравнения прямой y = а + bx, если а = 0, а b = 1, то есть y = 0 + 1x = х.

Иными словами, уравнение у = х является уравнением биссектрисы угла, которое делит координатную плоскость строго пополам; тангенс такого угла равен единице: какое значение задаем на оси ОХ, такое же значение получим и по оси OY. И если свободный член уравнения прямой отражает пересечение оси OY в точке 0 на оси OX, то коэффициент при аргументе «х» отражает скорость изменения функции «у».

Действительно, если при увеличении х величина у возрастает (рис. 3, 5), то значение b > 0, скорость изменения у положительна. И наоборот: если при увеличении х величина у убывает (рис. 2), то значение b < 0, скорость изменения у отрицательна. Если же при увеличении х величина у остается без изменений (рис. 6), то значение b = 0, скорость изменения у равна нулю или отсутствует: y = const.

Итак, после того, как искомые коэффициенты уравнения линейной регрессии а и b найдены и прогноз построен, для завершения поставленной задачи остается оценить точность аппроксимации, вычислить величину коэффициента линейной корреляции, а также оценить значимость полученных коэффициентов и надежность уравнения в целом.