Доказательство. Рассмотрим последовательность {xn} с общим членом

Лекция 18

Число е

Рассмотрим последовательность {x_n} с общим членом .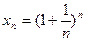

Докажем, что она сходится.

Для этого достаточно доказать:

1) {x_n} возрастающая;

2) {x_n} ограничена сверху.

Рассмотрим 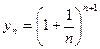и докажем, что последовательность {y_n} убывает, т.е .

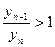Докажем, что она сходится.

Доказательство

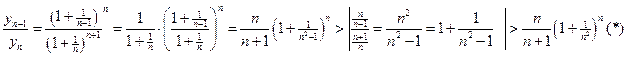
Замечание1. Неравенство (*) верно: знаменатель увеличили, дробь уменьшилась.

Обозначим .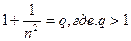

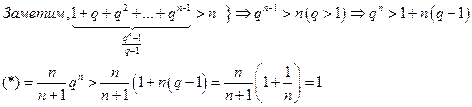
Итак, 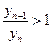, т.е. последовательность {y_n} убывающая.

Так как 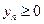, то последовательность ограничена, т.е. существует предел последовательности .

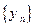Замечание2. В доказательстве использовалась формула суммы бесконечно убывающей геометрической последовательности: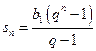

Обозначим …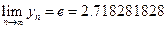

Таким образом .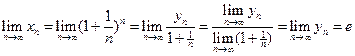

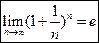называют вторым замечательным пределом