Эллипс. Определение эллипса и вывод его конического уравнения

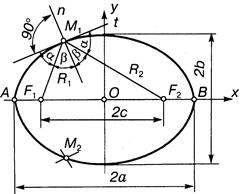
Эллипс – это плоская кривая (множество точек плоскости), для произвольной точки которой (точка М рис. 46) сумма расстояний до двух фиксированных точек (фокусов F₁ и F₂) есть величина постоянная и равная длине большой оси эллипса - 2а (рис. 13.51). Расстояние между фокусами F₁ и F₂ равняется 2с, его называют фокусным. Длина малой оси эллипса равняется 2b. Точка пересечения осей эллипса является его центром, концы осей — вершинами эллипса.

В соответствии с определением эллипса и принятых условных обозначений можно доказать, что требуется, чтобы сумма расстояний до двух фиксированных точек (фокусов F₁ и F₂), являющихся величиной постоянной должна быть больше расстояния между фокусами.

F₁M + F₂M = 2а (1)

F₁M + F₂M >F₁F₂,

то 2а > 2с,

т. е. а > с (2)

Из определения эллипса непосредственно вытекает следующий способ построения его при помощи нити: если концы не­растяжимой нити длины 2а закрепить в точках F₁, F₂ и на­тянуть нить острием карандаша, то при движении острия оно будет вычерчивать эллипс с фокусами F₁, F₂ и суммой фокальных радиусов 2а. Выполнив это построение факти­чески, можно наглядно убедиться, что эллипс представляет собой выпуклую замкнутую линию (овал), симметричную от­носительно прямой F₁F₂ а также относительно прямой, ко­торая проходит перпендикулярно к отрезку F₁F₂ через его середину (рис. 46).

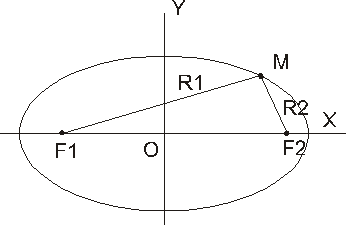
Рис.46.

В AutoCAD для построения эллипса имеются две команды из меню «Рисование-Эллипс»: «По центру» и «Ось, конец». При использовании команды «По центру» параметрами являются координаты точки центра О, конца большей оси А, конца меньшей оси В. Таким образом отрезок ОВ является меньшим радиусом R₂, а отрезок ОА – большим радиусом R₁. При использовании команды «Ось конец» параметрами являются начальная и конечная координаты одной из осей, и координата любого конца другой оси.

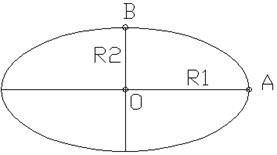
Пример построения эллипса

Установить форму эл­липса можно аналитически при помощи исследования его уравнения.

Пусть дан какой-нибудь эллипс с фоку­сами F₁, F₂ (вместе с тем мы считаем данными а и с). Введем на плоскости декартову прямоуголь­ную систему координат, оси которой расположим специальным образом по отношению к этому эллипсу; имен­но, в качестве оси абсцисс мы возьмем прямую F₁F₂, считая ее направленной от F₁ к F_{2 ,} начало координат поместим в середине отрезка F₁F₂ (рис. 46). Выведем уравнение эллип­са в установленной системе координат.

Возьмем на плоскости произвольную точку М и обо­значим ее координаты через х и у. Обозначим, далее, через r₁ и r₂ расстояния от точки М до фокусов (r₁ = F₁М, r₂ = F₂М). Точка М будет находиться на данном эллипсе в том и только в том случае, когда r₁ + r₂ = 2а. (3)

Чтобы получить искомое уравнение, нужно в равенстве (3) заменить переменные r₁ и r₂ их выражениями через коорди­наты х, у.

Заметим, что, так как F₁F₂ =2c и так как фокусы F₁ и F₂ расположены на оси Ох симметрично относительно начала координат, то они имеют соответственно координаты (-с; 0) и (+с; 0); приняв это во внимание и применяя формулу (2), находим:

r₁ = 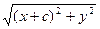, r₂ = 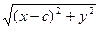^. (4)

Заменяя r₁ и r₂ в равенстве (3) найденными выражениями, получаем:

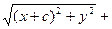
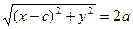(5)

Это и есть уравнение рассматриваемого эллипса в назначенной системе координат, так как ему удовлетворяют координаты точки М (х; у) в том и только в том случае, когда точка М лежит на этом эллипсе. Дальнейшие наши выкладки имеют целью получить уравнение эллипса в более простом виде.

Поместим в уравнение (5) первый радикал, после чего возведем обе части равенства в квадрат, получим:

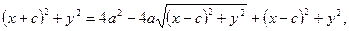(6)

или

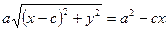(7)

Возводя в квадрат обе части последнего равенства, найдем:

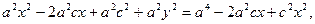(8)

откуда

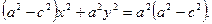(9)