Теоретический тест-тренинг №1
1. Если событие А исключает появление события В, то такие события называются
1) несовместными 2)независимыми 3)противоположными
4) совместными 5)равновозможными
2. Установите соответствие между понятием и его определением
| А невозможное | 1. событие, которое всегда происходит в условиях определенного опыта |
| Б случайное | 2. событие, которое никогда не происходит в условия определенного опыта |
| В противоположное | 3. событие, которое происходит только тогда, когда исходное событие не происходит |
| 4. событие, которое может произойти, а может и не произойти в условиях определенного опыта |
3. На рисунке 1.1 изображена операция с событиями.
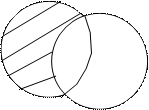 |
А В
Рис.1.1. Операция с событиями А и В.
Этой операцией является:
1) А∩В 2) АUВ 3) А\В 4) 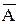 5)В\А
5)В\А
4. Вероятность достоверного события равна
1) 0 2) 1 3) –1 4) ∞ 5) любое число
5. Число перестановок элементов множества в случае, когда не все элементы различны, определяют по формуле:
1) 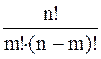 2)
2) 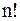 3)
3) 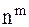 4)
4) 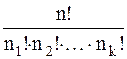 5)
5) 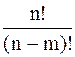
6. Дайте классическое определение вероятности. Перечислите недостатки этого определения.
7. Сформулируйте теорему о вероятности суммы совместных событий. Перечислите последовательность действий при доказательстве этой теоремы:
Теоретический тест – тренинг №2
1. Если вероятность появления события А меняется в зависисмости от того произошло событие В или нет, то такие события называются
1) несовместными 2)независимыми 3)противоположными
4) зависимыми 5)равновозможными
2. Установите соответствие между понятием и его определением
| А невозможное | 1. событие, которое всегда происходит в условиях определенного опыта |
| Б противоположное | 2. событие, которое никогда не происходит в условия определенного опыта |
| В достоверное | 3. событие, которое происходит только тогда, когда исходное событие не происходит |
| 4. событие, которое может произойти, а может и не произойти в условиях определенного опыта |
3. На рисунке 1.2 изображена операция с событиями.
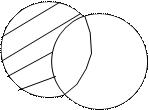 |
В А
Рис.1.2. Операция с событиями А и В.
Этой операцией является:
1) А∩В 2) АUВ 3) А\В 4) 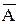 5)В\А
5)В\А
4. Вероятность невозможного события равна
1) 0 2) 1 3) –1 4) ∞ 5) любое число
5. Число сочетаний из n элементов по m элементов в каждом в случае, когда все элементы различны, определяют по формуле:
1) 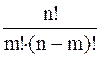 2)
2) 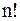 3)
3) 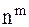 4)
4) 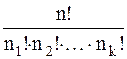 5)
5) 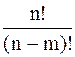
6. Дайте статистическое определение вероятности. Укажите условия существования статистической вероятности.
7. Сформулируйте теорему о о вероятности совместного появления двух событий. Перечислите действия при доказательстве этой теоремы.
Теоретический тест – тренинг №3
1. Если событие А не исключает появления события В, то такие события называются
1) несовместными 2)независимыми 3)противоположными
4) совместными 5)равновозможными
2. Установите соответствие между понятием и его определением
| А случайное | 1. событие, которое всегда происходит в условиях определенного опыта |
| Б противоположное | 2. событие, которое никогда не происходит в условия определенного опыта |
| В достоверное | 3. событие, которое происходит только тогда, когда исходное событие не происходит |
| 4. событие, которое может произойти, а может и не произойти в условиях определенного опыта |
3. На рисунке 1.3 изображена операция с событиями.
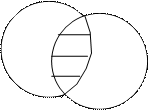 |
А В
Рис.1.3. Операция с событиями А и В.
Этой операцией является:
1) А∩В 2) АUВ 3) А\В 4) 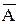 5)В\А
5)В\А
4. Значения вероятности случайного события заключены в промежутке:
1) (–∞; – 1) 2) (5, +∞) 3) [–1; 0)
4) [0, 1] 5) (1; 5]
5. Число размещений из n элементов по m элементов в каждом в случае, когда не все элементы различны, определяют по формуле:
1) 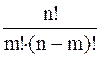 2)
2) 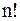 3)
3) 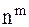
4) 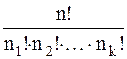 5)
5) 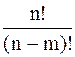
6. Дайте определение геометрической вероятности. Приведите примеры. Перечислите недостатки определения.
7. Сформулируйте теорему о формуле полной вероятности. Перечислите последовательность действий при выводе формулы.
Теоретический тест – тренинг №4
1. Если вероятность появления события А не изменяется в зависимости от того произошло событие В или нет, то такие события называются
1) несовместными 2)независимыми 3)противоположными
4) зависимыми 5)равновозможными
2. Установите соответствие между понятием и его определением
| А невозможное | 1. событие, которое всегда происходит в условиях определенного опыта |
| Б случайное | 2. событие, которое никогда не происходит в условия определенного опыта |
| В достоверное | 3. событие, которое происходит только тогда, когда исходное событие не происходит |
| 4. событие, которое может произойти, а может и не произойти в условиях определенного опыта |
3. На рисунке 1.4 изображена операция с событиями.
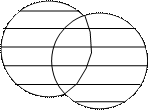 |
А В
Рис.1.4. Операция с событиями А и В.
Этой операцией является:
1) А∩В 2) АUВ 3) А\В 4) 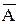 5)В\А
5)В\А
4. Если вероятность события А равна p, то вероятность противоположного события 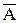 равна
равна
1)1 + р 2)1 – р 3)1 4)0 5)любое число
5. Число перестановок элементов множества в случае, когда все элементы различны, определяют по формуле:
1) 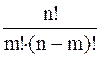 2)
2) 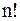 3)
3) 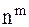 4)
4) 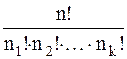 5)
5) 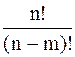
6. Перечислите аксиомы вероятности.
7. Сформулируйте теорему о вероятности появления хотя бы одного из событий, независимых в совокупности. Перечислите последовательность действий при доказательстве этой теоремы.
 2015-06-16
2015-06-16 861
861








