Устойчивость САУ. Математический критерий устойчивости. Линеаризация САУ

Устойчивость представляет собой способность системы автоматического регулирования возвращаться к исходному состоянию после кратковременного внешнего воздействия. Системы автоматического регулирования, как правило, должны быть устойчивыми.

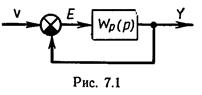
Необходимым и достаточным условием устойчивости линейной системы автоматического регулирования является отрицательность вещественных частей всех корней ее характеристического уравнения. Последнее может быть получено из передаточной функции замкнутой системы, связывающей любые ее вход и выход, путем приравнивания нулю знаменателя передаточной функции. На рис. 7.1 показана структурная схема, к которой может быть приведена любая односвязная линейная система автоматического регулирования при отсутствии всех внешних воздействий, кроме задающего. Если передаточная функция разомкнутой системы

,

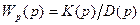где К (р) и D (р) -полиномы степеней соответственно m и n (m£n), то передаточная функция замкнутой системы

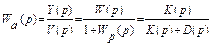
откуда путем приравнивания знаменателя W_а(р) нулю получается характеристическое уравнение замкнутой системы n-й степени:

.

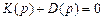Обозначая ,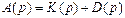

можно записать характеристическое уравнение в виде

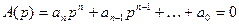
Попытки анализа устойчивости линейных систем автоматического регулирования путем прямого отыскания корней характеристического уравнения наталкиваются на практические трудности, связанные с отсутствием аналитических выражений для корней уравнений степени выше четвертой; для уравнений третьего и четвертого порядков имеющиеся выражения малоудобны. Однако нет необходимости находить значения корней, поскольку для суждения об устойчивости системы нужно знать лишь, что все они расположены левее мнимой оси на плоскости комплексного переменного р. В теории автоматического регулирования пользуются условиями, которые позволяют судить о расположении корней в левой полуплоскости без нахождения их значений; эти условия называются критериями устойчивости.

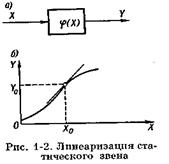
Главным упрощением, к которому следует стремиться при выводе уравне­ний звеньев системы, является их линеаризация, т. е. описание линейными дифференциальными урав­нениями. Линеаризация нелинейности, содержащейся в уравнении звена, зак­лючается в замене этой нелинейности приближенной линейной зависимостью. Рассмотрим звено, описываемое не­линейной статической зависимостью Y=Ф(X) (рис. 1-2, а). Пусть устано­вившийся режим звена соответствует значениям входной и выходной вели­чин Х₀ и У₀ (рис. 1-2, б) и отклонения X от Х0 в процессе работы звена доста­точно малы. В этом случае исходную нелинейную зависимость Y=Ф(X) можно разложить в ряд Тейлора в окрестностях точки установившегося режима и, отбросив члены ряда выше первого порядка малости, получить следующую приб­лиженную зависимость:

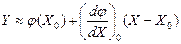
где 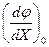- значение производной функции Ф(X) по X при подстановке в выражение этой производной X=Х₀.

Это уравнение можно переписать в таком окончательном виде: ,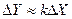

где DХ=Х-Х₀; DУ=У-У₀; .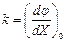

Проведенная линеаризация имеет простую графическую интер­претацию: она соответствует, как показано на рис. 1-2, б, замене действительной нелинейной характеристики касательной к ней в точке, соответствующей установившемуся режиму. Коэффи­циент k в уравнении (1-2) равен тангенсу угла наклона этой касательной относительно оси абсцисс. Поэтому его величина может быть найдена чисто графическим построением.