Решение. Опустим перпендикуляр из В1К на плоскость ABC1

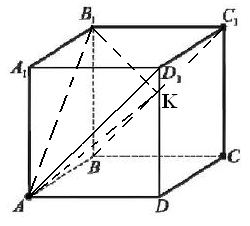
Опустим перпендикуляр из В₁К на плоскость ABC₁. К – центр ВВ₁СС₁, так как В₁К перпендикулярна ВС₁ и D₁C₁.

Тогда искомый угол между прямой AВ₁ и плоскостью ABC₁ это .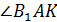

Пусть сторона куба равна a. Тогда по теореме Пифагора:

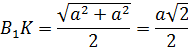
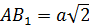
Тогда из прямоугольного треугольника:

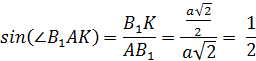
Отсюда: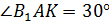

Ответ: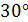

№10

В основании прямой призмы ABСA₁B₁C₁ лежит прямоугольный треугольник АВС, у которого угол С равен 90 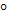, угол А равен 30 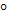, AC = 10 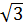. Диагональ боковой грани B₁C составляет угол 30 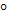с плоскостью AA₁B₁. Найдите высоту призмы.