Приведем уравнение к виду:
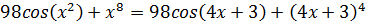
Рассмотрим непрерывную функцию:
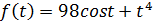
Данная функция определена для любого значения аргумента, чётная, так как f(-t) = f(t). Найдём её производную:
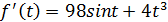
при 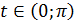
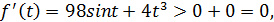
а при 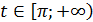
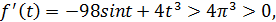
Таким образом, 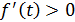 при
при 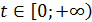 , следовательно, f(t) возрастает на этом промежутке. Значит, каждое своё значение из множества значений E(f), кроме f(0), функция принимает в двух симметричных относительно t = 0 точках, а стало быть, уравнение
, следовательно, f(t) возрастает на этом промежутке. Значит, каждое своё значение из множества значений E(f), кроме f(0), функция принимает в двух симметричных относительно t = 0 точках, а стало быть, уравнение 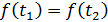 равносильно уравнению
равносильно уравнению 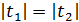 . Записав исходное уравнение в виде
. Записав исходное уравнение в виде 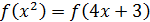 , получим
, получим
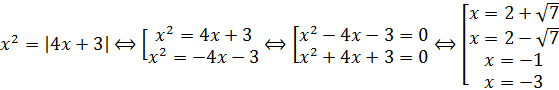
Ответ: 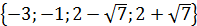
№16
Решить уравнение:
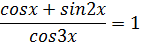
 2015-06-16
2015-06-16 282
282








