а) Решение уравнения 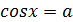 :
:
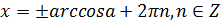
Тогда для нашего уравнения:
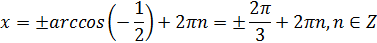
Изобразим корни уравнения графически:
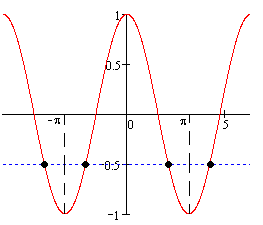
б) Отметим отрезок [0; π]:
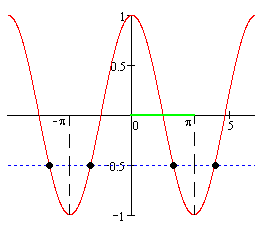
Из рисунка видно, что отрезку [0; π] принадлежит один корень: 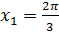
в) Отметим отрезок 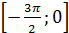 :
:
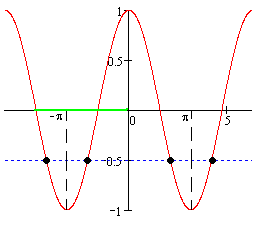
Из рисунка видно, что отрезку 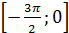 принадлежат два корня:
принадлежат два корня: 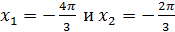
г) Корни принадлежащие отрезку [-2π;3π] найдем из неравенства:
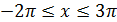
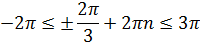
Последнее неравенство распадается на два:
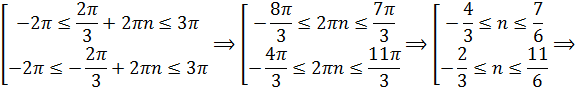
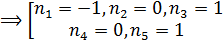
Искомые корни:
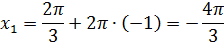
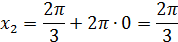
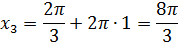
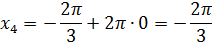
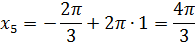
Ответ: а) 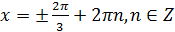 ; б)
; б) 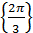 ; в)
; в) 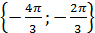 ; г)
; г) 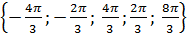 .
.
№2
Найдите те решения уравнения 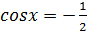 , для которых sin x > 0.
, для которых sin x > 0.
Решение.
Решение уравнения 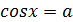 :
:
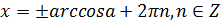
Тогда для нашего уравнения:
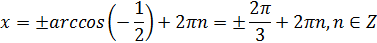
Изобразим решение неравенства sin x > 0 графически:
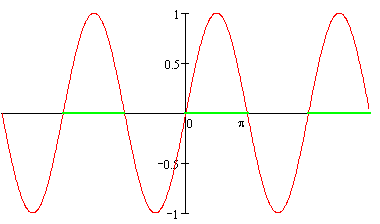
Затем отметим корни уравнения 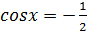 :
:
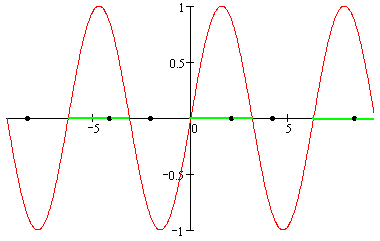
Как видим на промежутке [0; 2π] длина которого 2π, неравенству
sin x > 0 удовлетворяет одно число 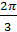 . Следовательно, все числа вида
. Следовательно, все числа вида 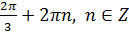 являются решениями уравнения
являются решениями уравнения 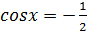 , для которых
, для которых
sin x > 0.
Ответ: 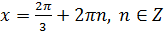
№3
Найдите наибольший отрицательный корень уравнения
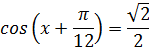
Решение.
Решение уравнения 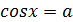 :
:
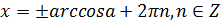
Следовательно:
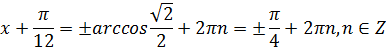
Отсюда:
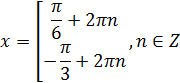
Из первой строчки наибольший отрицательный: 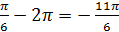 , из второй:
, из второй: 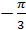 . Следовательно, наибольшим отрицательным является:
. Следовательно, наибольшим отрицательным является: 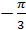 .
.
|
|
|
Ответ: 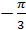 .
.
№4
Найдите корни уравнения
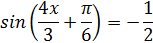
принадлежащие промежутку [-2π; 2π).
Решение.
Решение уравнения 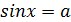 :
:
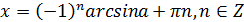
Тогда для нашего уравнения имеем:
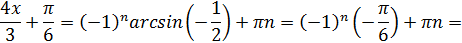
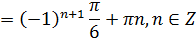
Отсюда:
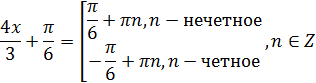
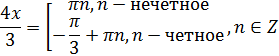
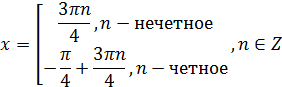
Представим n следующим образом:
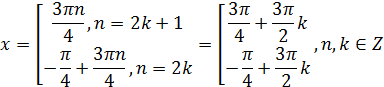
Корни, принадлежащие отрезку [-2π; 2π] найдем из неравенств:
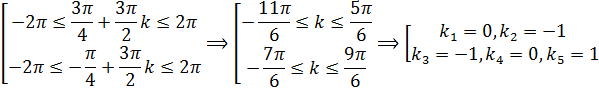
Тогда:
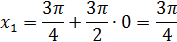
ar w:top="1417" w:right="1417" w:bottom="1417" w:left="1417" w:header="708" w:footer="708" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 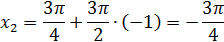
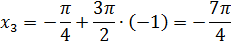
ar w:top="1417" w:right="1417" w:bottom="1417" w:left="1417" w:header="708" w:footer="708" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 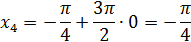
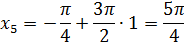
Ответ: 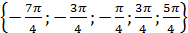
№5
Решить уравнение:
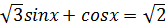
Решение.
Данное уравнение равносильно со следующим:
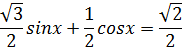
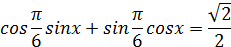
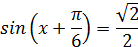
Отсюда получаем:
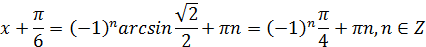
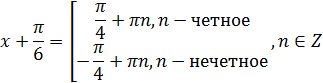
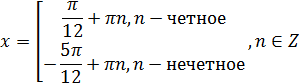
Представим n следующим образом:
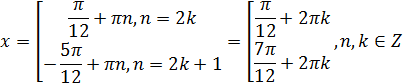
Ответ: 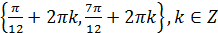
№6
Найдите корни уравнения
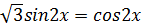
принадлежащие отрезку [-1;4].
Решение.
Данное уравнение равносильно со следующим:
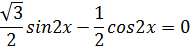
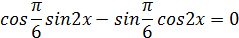
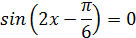
Отсюда:
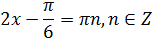
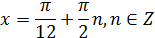
Корни, принадлежащие отрезку [-1;4] найдем из неравенства:
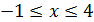
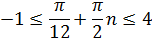
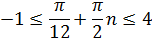
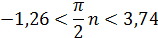
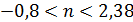
Отсюда: 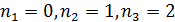 искомые корни:
искомые корни:
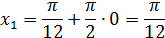
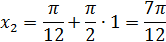
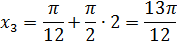
Ответ: 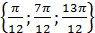
№7
Решить уравнение:
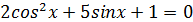
 2015-06-16
2015-06-16 310
310








