Два конечных множества могут содержать одинаковое или разное число элементов. Возникает вопрос: равно ли число элементов в двух множествах? Есть два способа выяснить это:
1. Пересчитать элементы и сравнить результаты.
2. Установить биекцию между этими двумя множествами. Если биекция возможна, то число элементов одинаковое.
Для бесконечного множества невозможно указать число элементов, но существует аналог понятия числа элементов для бесконечного множества. Если между элементами двух бесконечных множеств можно установить биекцию, то говорят, что эти множества эквивалентны или имеют одинаковую мощность, Мощность характеризуется так называемым координальным числом. Это символ, обозначающий мощность класса эквивалентных множеств.
Множество эквивалентное множеству натуральных чисел называется счетным и характеризуется координальным числом 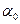 .
.
Теоремы о счетных множествах:
Теорема 1. Всякое бесконечное множество А, содержит счетное собственное подмножество.
Теорема 2 Всякое счетное множество А1 можно представить в виде дизъюнктивной суммы двух счетных подмножеств А1 и А2.
Сумма А1 + А2 называется дизъюнктивной, если
- А1
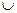 А2=А
А2=А - А1
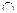 А2 =Æ
А2 =Æ
Теорема3. Из всякого бесконечного множества М можно извлечь собственное подмножество А, эквивалентное самому множеству (т.е. часть целого = самому целому).
Из теоремы 3 можно дать определение бесконечного множества.
Если существует собственное подмножество эквивалентное самому множеству, то множество называется бесконечным.
Теорема 4. Счетная сумма счетных множеств – есть счетное множество.
Теорема Кантора. Множество всех подмножеств данного множества обладает большей мощностью, чем данное множество. (Для каждого множества можно построить новое множество большей мощностью, чем исходное).
Теорема Кантора доказывает существование бесконечных множеств большей мощностью, чем счётное множество.
Теорема Кантора - Беринштейна: Пусть даны такие два множества А и В, что существуют В1 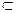 В такое что А~В, и существует А1
В такое что А~В, и существует А1 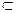 А такое что А1 ~В, тогда А~В.
А такое что А1 ~В, тогда А~В.
Т.е. если из двух множеств каждое эквивалентно собственному подмножеству другого множества, то сами множества эквивалентны.
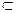 - подмножество, ~ - эквивалентность
- подмножество, ~ - эквивалентность
 2015-06-04
2015-06-04 3876
3876
