Отображение множеств

Пусть даны два произвольных множества Х, Y. Закон, по которому каждому элементу множества Х ставится в соответствие один и только один элемент из множества Y называется отображением множества Х в Y и обозначается f: Х 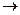Y

Множество Х называется областью определения отображения f. Все элементы y 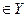, которому поставлено в соответствие некоторый элемент 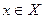образуют множество f(x) называется образом множества X при отображении f.

х у

.

Множество всех 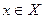, которому соответствует некоторый элемент y 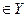, называется прообразом элемента y 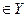и обозначается 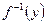f^--1 (y)={x|f(x) 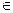у} (или обратное отображение).

Справедливо 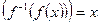, f(x)≤ Y

Если 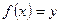, то отображение f называется сюръекцией (или отображение на множество Y).

.

cюръекция инъекция биекция

Если из 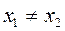следует, что 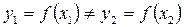, то отображение f называется инъекцией (или взаимнооднозначным отображением множества Х в множество У).

Т.е. при инъекции разным Х соответствуют разные У

Отображения одновременно являющееся сюръекцией и инъекцией называется биекцией.

Если множества Х и Y числовые, то f называется функцией