Множество М с определенной на этом множестве операцией f называется алгеброй и обозначается 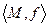 . Операций на множестве может быть несколько.
. Операций на множестве может быть несколько. 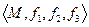
Операция f называется n-арной, если она всякой упорядоченной системе из n -элементов ставит в соответствии один элемент из того же множества М; обозначают 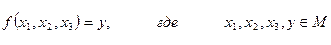
Одноарной называется операция, которая одному элементу ставит в соответствие один элемент.
n –арная операция называется коммутативной, если ее результат не зависит от порядка элементов
т.е. 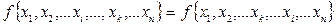 при
при 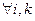
Если операция, определенная на множестве М – коммутативная, то алгебра называется коммутативной. Обозначим 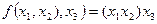
Если 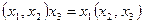 , то операция f называется ассоциативной
, то операция f называется ассоциативной
Множество М, на котором определена ассоциация бинарная, операция называется полугруппой.
Элемент 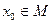 называется левым (правым) единичным элементом для операции f, если для
называется левым (правым) единичным элементом для операции f, если для 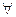
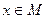 справедливо
справедливо 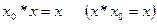
Полугруппа, в которой есть единичный элемент, называется маноидом.
Элемент 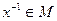 называется обратным левым (правым), если
называется обратным левым (правым), если 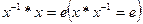 .
.
Маноид, в котором для любого 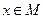 существует
существует 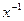 называется группой.
называется группой.
Пример: Определить образует ли группу множество четных натуральных чисел относительно сложения 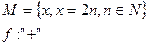
1. Ассоциативность: (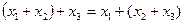 )
)
2. единичный элемент 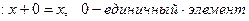
3. обратный элемент: 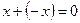 , -х – противоположное число
, -х – противоположное число
Все 3 условия выполняются, значит М – группа.
Две группы М, Р называются изоморфными, если существует биекция 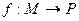 , которая сохраняет операцию умножения в группе. Т.е. для
, которая сохраняет операцию умножения в группе. Т.е. для 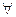
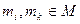 справедливо
справедливо 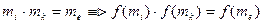
 2015-06-04
2015-06-04 1127
1127
