Производная от функции  является также функцией от
является также функцией от  и может быть дифференцируема.
и может быть дифференцируема.
Производная от производной функции  называется производной второго порядка или второй производной функции и обозначается:
называется производной второго порядка или второй производной функции и обозначается: 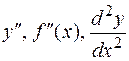 . Таким образом,
. Таким образом,
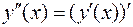 .
.
Вторая производная имеет простой механический смысл. Пусть 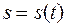 — закон движения материальной точки, тогда первая производная определяет скорость движения
— закон движения материальной точки, тогда первая производная определяет скорость движения 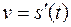 . Вторая же производная есть скорость изменения скорости движения, т. е. ускорение
. Вторая же производная есть скорость изменения скорости движения, т. е. ускорение 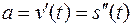 .
.
Аналогично вводятся производные третьего, четвертого и более высоких порядков.
Производной 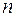 -го порядка от функции
-го порядка от функции  называется производная от производной (
называется производная от производной (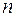 – 1)-го порядка.
– 1)-го порядка.
Рассмотрим примеры нахождения производных высших порядков.
Пример. Найти производную 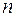 -го порядка от функции
-го порядка от функции 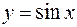 .
.
Решение. Выполняя последовательное дифференцирование, находим:
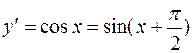
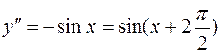
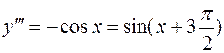
....................
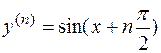 .
.
 2015-06-04
2015-06-04 453
453








