Пусть функция  задана уравнением
задана уравнением 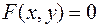 . В этом случае говорят, что функция
. В этом случае говорят, что функция 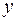 задана неявно. Предположим, что функция
задана неявно. Предположим, что функция 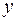 дифференцируема. Если в уравнении
дифференцируема. Если в уравнении 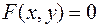 под
под 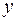 подразумевать функцию
подразумевать функцию 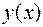 , то это уравнение обращается в тождество по аргументу
, то это уравнение обращается в тождество по аргументу  :
: 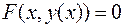 . Дифференцируем его по
. Дифференцируем его по  , считая, что
, считая, что 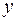 есть функция
есть функция  . Получаем новое уравнение, содержащее
. Получаем новое уравнение, содержащее  ,
, 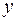 и
и 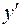 . Разрешая его относительно
. Разрешая его относительно 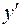 , находим производную искомой функции
, находим производную искомой функции  , заданной в неявном виде.
, заданной в неявном виде.
Пример. Найти производную функции 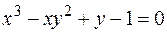 , заданной неявно.
, заданной неявно.
Решение. Дифференцируя по  неявную функцию и считая, что
неявную функцию и считая, что 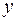 — функция от
— функция от  , имеем
, имеем 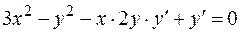 ,
,
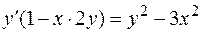 ,
,
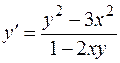 .
.
Отметим, что в этом случае 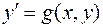 .
.
По определению вторая производная от функции  есть производная от первой производной. Следовательно, для нахождения второй производной надо продифференцировать найденную первую производную по аргументу
есть производная от первой производной. Следовательно, для нахождения второй производной надо продифференцировать найденную первую производную по аргументу  , продолжая рассматривать
, продолжая рассматривать 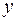 как функцию от
как функцию от  . В выражение для второй производной в общем случае войдут
. В выражение для второй производной в общем случае войдут  ,
, 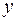 и
и 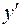 . Подставляя вместо
. Подставляя вместо 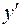 его значение, находим
его значение, находим 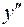 , зависящую только от
, зависящую только от  и
и 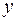 . Аналогично поступаем при нахождении производных более высоких порядков.
. Аналогично поступаем при нахождении производных более высоких порядков.
Пример. Найти производную второго порядка от функции  , заданной уравнением
, заданной уравнением 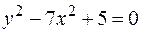 .
.
Решение. Найдем первую производную
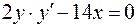
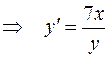 .
.
Дифференцируя данное уравнение вторично, получаем 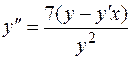 .
.
Так как 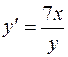 , имеем
, имеем 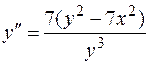 .
.
 2015-06-04
2015-06-04 530
530








