Производная алгебраической суммы конечного числа дифференцируемых функций равна алгебраической сумме производных отдельных слагаемых.
Доказательство. Рассмотрим функцию 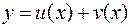 . Дадим фиксированному значению аргумента
. Дадим фиксированному значению аргумента  приращение
приращение 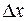 . Тогда функции
. Тогда функции 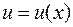 и
и 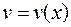 получат приращения
получат приращения 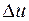 и
и 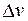 , а функция
, а функция 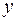 — приращение
— приращение 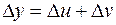 . Таким образом, по определению
. Таким образом, по определению
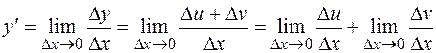 .
.
Так как по предположению функции 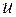 и
и 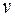 дифференцируемы,
дифференцируемы,
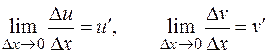 .
.
Следовательно,
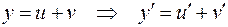 .
.
Это правило легко обобщается на случай любого конечного числа слагаемых
⊠
Правило дифференцирования произведения функций. Производная произведения двух дифференцируемых функций равна сумме произведений производной первого сомножителя на второй и производной второго сомножителя на первый, т. е.
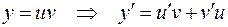 .
.
Доказательство. Пусть 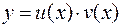 . Когда аргументу
. Когда аргументу  придают приращение
придают приращение 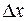 , то функции
, то функции 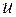 ,
, 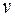 и
и 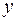 получают соответственно приращения
получают соответственно приращения 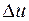 ,
, 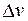 и
и 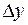 , причем
, причем
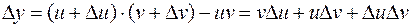 .
.
Разделим последнее равенство на 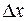
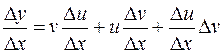 .
.
В последнем равенстве приращения 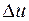 ,
, 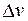 и
и 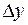 зависят от
зависят от 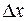 , а
, а 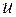 и
и 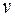 не зависят от
не зависят от 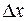 (так как
(так как 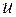 и
и 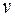 — значения функции, соответствующие начальному значению аргумента
— значения функции, соответствующие начальному значению аргумента  ).
).
Используя теоремы о пределах функций, находим
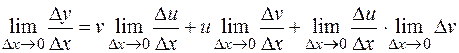 .
.
Так как
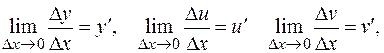
и 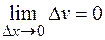 (т.к. функция
(т.к. функция 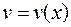 непрерывна). Итак, окончательно имеем:
непрерывна). Итак, окончательно имеем:
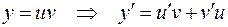 .
.
⊠
Следствие. Пусть функция 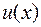 имеет производную в точке
имеет производную в точке  , тогда функция
, тогда функция 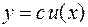 (
(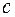 — const) также имеет в этой точке производную, причем
— const) также имеет в этой точке производную, причем
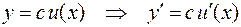 .
.
Правило дифференцирования произведения двух функций методом математической индукции легко можно распространить на случай любого конечного числа сомножителей
Правило дифференцирования частного функций. Производная дроби (частного двух дифференцируемых функций) равна дроби, у которой знаменатель есть квадрат знаменателя данной дроби, а числитель представляет собой разность между произведением знаменателя данной дроби на производную ее числителя и произведением числителя на производную знаменателя.
Доказательство аналогично доказательству предыдущих двух теорем.
Пример. Найти производную функции 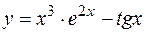 .
.
Решение. 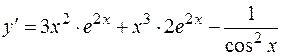 .
.
 2015-06-04
2015-06-04 4011
4011
