Теорема. Если функция  монотонна на отрезке
монотонна на отрезке 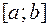 и имеет во всех точках интервала
и имеет во всех точках интервала 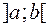 ненулевую производную
ненулевую производную 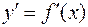 , то обратная функция
, то обратная функция 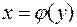 дифференцируема во всех точках интервала
дифференцируема во всех точках интервала 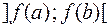 и для любого
и для любого 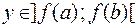 ее производная равна
ее производная равна 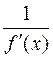 .
.
Доказательство. Пусть функция  монотонна на отрезке
монотонна на отрезке 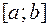 и имеет производную
и имеет производную 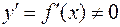 . Пусть, далее,
. Пусть, далее, 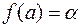 ,
, 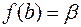 . Тогда существует обратная (по отношению к функции
. Тогда существует обратная (по отношению к функции  ) функция
) функция 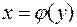 , которая является непрерывной и монотонной на
, которая является непрерывной и монотонной на 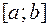 :
:

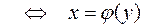 .
.
Дадим фиксированному значению аргумента 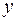 обратной функции приращение
обратной функции приращение 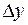 . Этому приращению соответствует приращение обратной функции, причем в силу ее монотонности
. Этому приращению соответствует приращение обратной функции, причем в силу ее монотонности 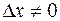 . Найдем производную обратной функции. По определению
. Найдем производную обратной функции. По определению
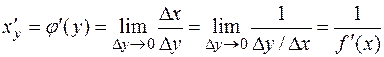 .
.
⊠
Пример. Найти производную функции, обратной данной 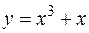 .
.
Решение. Даннаяфункция непрерывна и монотонна на всей числовой оси. Следовательно, существует, которая также является непрерывной и монотонной.
Найдем производную функции 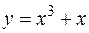 :
:
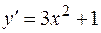 .
.
Следовательно,
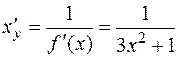 .
.
 2015-06-04
2015-06-04 557
557








