Пусть функция  задана параметрически:
задана параметрически:
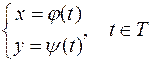 .
.
Найдем первую производную функции 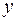 по переменной
по переменной  , то есть
, то есть
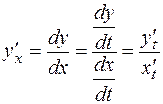 .
.
Т.е. 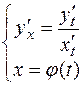 .
.
Найдем вторую производную от функции 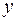 по переменной
по переменной  . Прямое дифференцирование функции
. Прямое дифференцирование функции 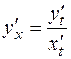 возможно только по параметру
возможно только по параметру 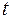 и даст в результате смешанную производную
и даст в результате смешанную производную 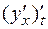 . Поэтому для нахождения второй производной от функции
. Поэтому для нахождения второй производной от функции 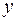 по переменной
по переменной  предварительно представим ее в виде:
предварительно представим ее в виде:
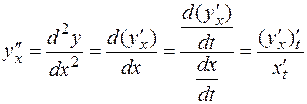
Тогда 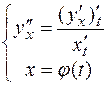 .
.
Аналогично находится третья производная:
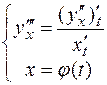
и производные высших порядков.
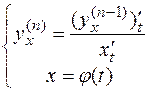
Пример. Найти производные первого и второго порядков от функции  , заданной параметрически:
, заданной параметрически:
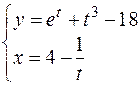 .
.
Решение. Найдем первую производную функции 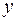 по переменной
по переменной  , то есть
, то есть
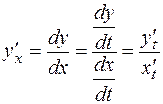 .
.
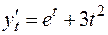 ,
, 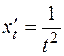 .
.
Следовательно 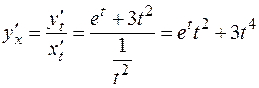 .
.
Найдем вторую производную от функции 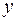 по переменной
по переменной  .
.
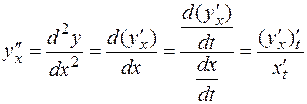 .
.
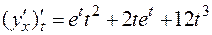 .
.
Следовательно 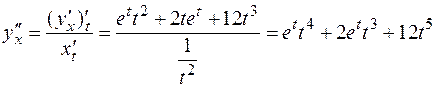 .
.
Ответ: 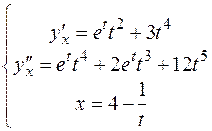 .
.
 2015-06-04
2015-06-04 3187
3187








