При исследовании поведения функции на бесконечности, т. е. при 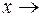 +¥ и при
+¥ и при 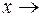 –¥, или вблизи точек разрыва второго рода часто оказывается, что расстояния между точками графика функции и точками некоторой прямой с теми же абсциссами сколь угодно малы. Такую прямую называют асимптотой графика.
–¥, или вблизи точек разрыва второго рода часто оказывается, что расстояния между точками графика функции и точками некоторой прямой с теми же абсциссами сколь угодно малы. Такую прямую называют асимптотой графика.
Различают асимптоты вертикальные (т. е. параллельные оси ординат) и наклонные. Частным случаем наклонной асимптоты является горизонтальная асимптота.
Прямая 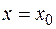 называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции  , если хотя бы один из односторонних пределов в точке
, если хотя бы один из односторонних пределов в точке  равен бесконечности, т. е.
равен бесконечности, т. е. 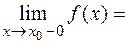 ¥ или
¥ или 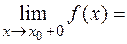 ¥.
¥.
Очевидно, что непрерывные на  функции вертикальных асимптот не имеют; такие асимптоты существуют только в точках разрыва второго рода функции
функции вертикальных асимптот не имеют; такие асимптоты существуют только в точках разрыва второго рода функции  . Следовательно, для отыскания вертикальных асимптот графика функции надо определить те значения
. Следовательно, для отыскания вертикальных асимптот графика функции надо определить те значения  , при которых хотя бы один из односторонних пределов функции бесконечен.
, при которых хотя бы один из односторонних пределов функции бесконечен.
Прямая 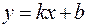 называется наклонной (если
называется наклонной (если  — горизонтальной) асимптотой графика функции
— горизонтальной) асимптотой графика функции  при
при 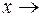 +¥ (
+¥ (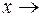 –¥), если функцию
–¥), если функцию  можно представить в виде
можно представить в виде 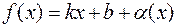 , где
, где 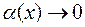 при
при 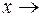 +¥ (
+¥ (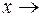 –¥).
–¥).
Теорема. Для того чтобы график функции  имел наклонную асимптоту
имел наклонную асимптоту 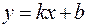 , необходимо и достаточно, чтобы существовали конечные пределы:
, необходимо и достаточно, чтобы существовали конечные пределы: 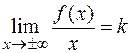 ,
, 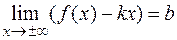 .
.
 2015-06-04
2015-06-04 782
782








