Теорема. (первый достаточный признак существования экстремума функции). Пусть  — критическая точка непрерывной функции
— критическая точка непрерывной функции  . Если
. Если  при переходе через точку
при переходе через точку  меняет знак с «+» на «—», то
меняет знак с «+» на «—», то  — точка локального максимума; если
— точка локального максимума; если  при переходе через точку
при переходе через точку  меняет знак с «—» на «+», то
меняет знак с «—» на «+», то  — точка локального минимума; если
— точка локального минимума; если  при переходе через точку
при переходе через точку  не меняет знак, то
не меняет знак, то  не является точкой локального экстремума.
не является точкой локального экстремума.
Доказательство. Пусть  — точка возможного экстремума, причем
— точка возможного экстремума, причем  >0
>0 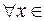
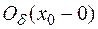 и
и  <0
<0 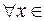
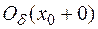 .
.
Тогда по теореме о достаточном признаке возрастания и убывания функции функция возрастает при 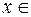
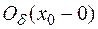 (т.е.
(т.е. 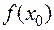 >
> 
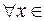
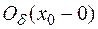 ) и убывает при
) и убывает при 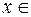
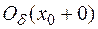 (т.е.
(т.е. 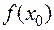 <
< 
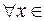
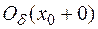 ),
),
т. е. точка  является точкой локального максимума.
является точкой локального максимума.
Аналогично доказывается и существование точки локального
минимума.
Если  сохраняет знак в окрестности точки
сохраняет знак в окрестности точки  , то в этой окрестности функция монотонна, т. е. точка
, то в этой окрестности функция монотонна, т. е. точка  не является точкой локального экстремума.
не является точкой локального экстремума.
⊠
На рисунке дана геометрическая интерпретация точки локального максимума.
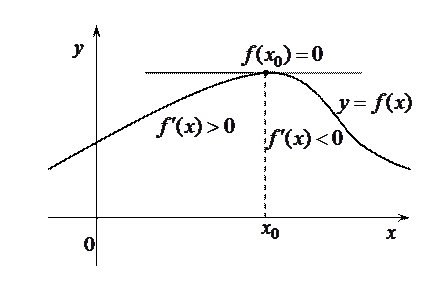
Теорема (второй достаточный признак существования экстремума функции). Стационарная точка  функции
функции  , дважды дифференцируемой в
, дважды дифференцируемой в 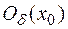 , является точкой локального минимума
, является точкой локального минимума  , если
, если 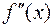 > 0, и точкой локального максимума, если
> 0, и точкой локального максимума, если 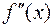 < 0.
< 0.
Доказательство. Пусть выполнены условия теоремы и 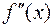 > 0. Тогда
> 0. Тогда  в
в 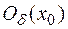 возрастает, но
возрастает, но 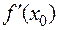 = 0, следовательно, в
= 0, следовательно, в 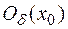 при переходе через точку
при переходе через точку 
 меняет знак с «—» на «+». Согласно первому достаточному признаку существования экстремума функции, точка
меняет знак с «—» на «+». Согласно первому достаточному признаку существования экстремума функции, точка  является точкой локального минимума функции
является точкой локального минимума функции  .
.
Если 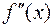 <0, то
<0, то  в
в 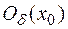 '(х) убывает, но
'(х) убывает, но  = 0, следовательно, в
= 0, следовательно, в 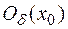 при переходе через точку
при переходе через точку 
 производная функции
производная функции  меняет знак с «+» на «—» Тогда, согласно первому достаточному признаку существования экстремума функции, точка
меняет знак с «+» на «—» Тогда, согласно первому достаточному признаку существования экстремума функции, точка  является точкой локального максимума функции
является точкой локального максимума функции  .
.
⊠
 2015-06-04
2015-06-04 2928
2928