Определение. График дифференцируемой функции  называется выпуклым вниз (или вогнутым) на
называется выпуклым вниз (или вогнутым) на  , если дуга кривой
, если дуга кривой  для
для 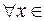
 расположена выше любой касательной, проведенной к графику этой функции.
расположена выше любой касательной, проведенной к графику этой функции.
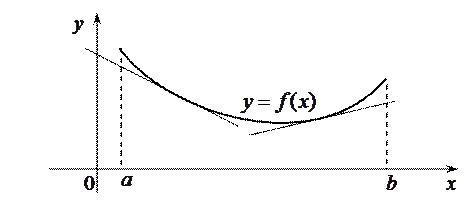
Определение. График дифференцируемой функции  называется выпуклым вверх (или выпуклым) на
называется выпуклым вверх (или выпуклым) на  , если дуга кривой
, если дуга кривой  для
для 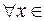
 расположена ниже любой касательной, проведенной к графику этой функции.
расположена ниже любой касательной, проведенной к графику этой функции.
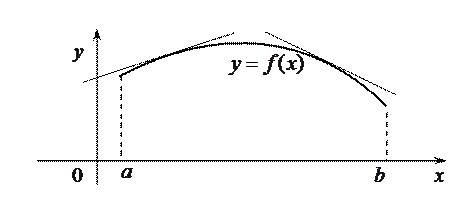
Определение. Точка 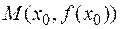 графика дифференцируемой функции
графика дифференцируемой функции  , в которой направление выпуклости меняется на противоположное, называется точкой перегиба.
, в которой направление выпуклости меняется на противоположное, называется точкой перегиба.
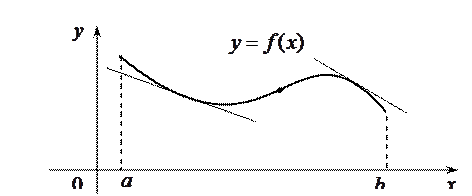
Теорема (достаточный признак вогнутости (выпуклости)). Если функция  на
на  дважды дифференцируема и
дважды дифференцируема и 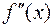 >0
>0 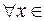
 , то график этой функции на
, то график этой функции на  вогнутый (выпуклый вниз). Если функция
вогнутый (выпуклый вниз). Если функция  на
на  дважды дифференцируема и
дважды дифференцируема и 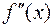 < 0
< 0 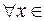
 , то график этой функции на
, то график этой функции на  выпуклый.
выпуклый.
Теорема. Если для функции  вторая производная
вторая производная 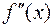 в некоторой точке
в некоторой точке  обращается в нуль или не существует и при переходе через нее меняет свой знак, то точка
обращается в нуль или не существует и при переходе через нее меняет свой знак, то точка 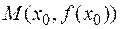 является точкой перегиба графика функции.
является точкой перегиба графика функции.
Доказательство. Пусть 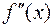 =0 или не существует. Если
=0 или не существует. Если 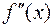 < 0 в
< 0 в 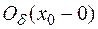 и
и 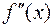 >0 в
>0 в 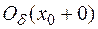 , то точка кривой с абсциссой
, то точка кривой с абсциссой  отделяет интервал выпуклости от интервала вогнутости. Если
отделяет интервал выпуклости от интервала вогнутости. Если 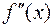 > 0 в
> 0 в 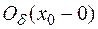 и
и 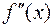 < 0 в
< 0 в 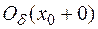 , то эта точка отделяет интервал вогнутости от интервала выпуклости кривой. В обоих случаях точка
, то эта точка отделяет интервал вогнутости от интервала выпуклости кривой. В обоих случаях точка 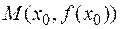 является точкой перегиба графика функции.
является точкой перегиба графика функции.
⊠
Пример. Найти интервалы выпуклости, вогнутости и точки перегиба графика функции 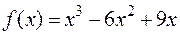 .
.
 Решение. Данная функция определена, непрерывна и дифференцируема на R, причем
Решение. Данная функция определена, непрерывна и дифференцируема на R, причем
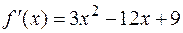 ,
,
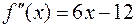 ,
,
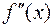 =0 при
=0 при 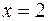 ,
,
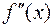 <0 при
<0 при 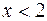 ,
,
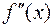 >0 при
>0 при 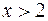 .
.
Следовательно, функция выпукла на интервале ]–¥; 2[, вогнута на интервале]2:+¥[, при 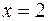
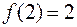 , точка
, точка 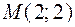 является точкой перегиба графика функции
является точкой перегиба графика функции 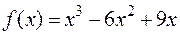 .
.
 2015-06-04
2015-06-04 787
787








