Теорема (третий достаточный признак существования экстремума функции)

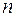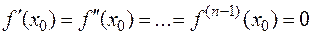Пусть функция — раз непрерывно дифференцируема в точке и , но 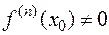. Тогда:

1) если 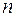— четное и 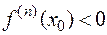то — точка локального макси­мума.

2) если 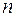— четное и 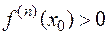, то — точка локального минимума;

3) если 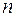— нечетное, то не является точкой локального экст­ремума.

Пример. Найти локальные экстремумы функции .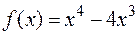

Решение. Данная функция определена, непрерывна и дифференцируема на . Найдем стационарные точки :

,

,

, .

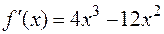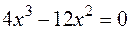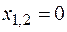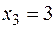1. Исследуем стационарную точку .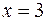

,

.

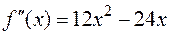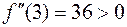Следовательно, по второму достаточному признаку существования экстремума функции стационарная точка 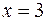является точкой локального минимума функции: .

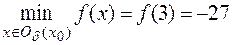2. Для исследования стационарной точки 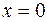находим

,

,

.

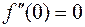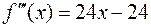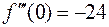Согласно третьему достаточному признаку существования экстремума функции, точка 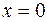не является точкой локального экстремума функции .