Решение. 1. Область определения (–¥; 1) Ç(1; +¥)

1. Область определения 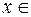(–¥; 1) Ç(1; +¥)

2. Так как

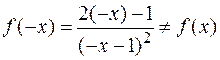и ,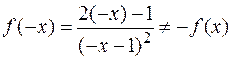

то исследуемая функция не является ни четной ни нечетной.

3. Функция не является периодической.

4. Точка 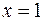является точкой разрыва второго рода, так как

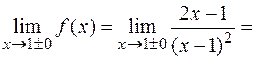+¥, а в остальных точках она непрерывна.

5. Найдем асимптоты графика функции:

а) Так как точка 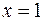является точкой разрыва второго рода, то прямая 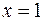и есть вертикальная асимптота.

б) Найдем наклонные асимптоты

,

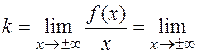
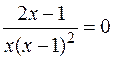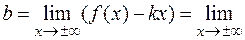
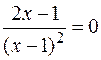
Следовательно, 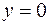наклонная (горизонтальная) асимптота.

6. Для нахождения участков монотонности и экстремаль­ных точек найдем первую производную функции:

.

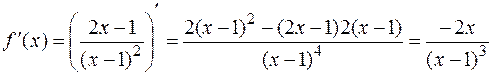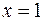Производная не существует при (точка разрыва, см. п. 4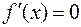) и при 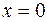. Область определения функции разобьем этими точками на интервалы (–¥, 0), (0, 1), (1, +¥) и определим знак в каждом из них. Результаты представим в виде таблицы

	(–¥, 0)		(0, 1)		(1, +¥)
	–		+	не сущ.	–
	Š	min	‰	точка разрыва	Š

На интервалах (–¥, 0), (1, +¥) функция убывает, на интервале (0, 1) функция возрастает, точка 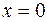— точка минимума.

.

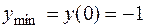7. Для нахождения участков выпуклости и вогнуто­сти найдем вторую производную функции

.

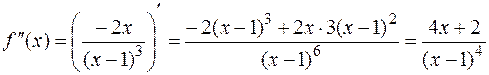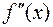не существует в точке 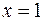(точка разрыва, см. п. 4) и равна нулю при 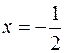. Область определения функции разобьем этими точками на интервалы (–¥, 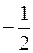), (, 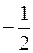1), (1, +¥) и определим знак 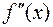в каждом из них. Результаты представим в виде таблицы

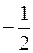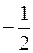
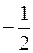	(–¥, )		(, 1)		(1, +¥)
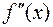
	–		+	не сущ.	+
	◠	перегиб	◡	точка разрыва	◡

На интервале (–¥, 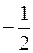) вторая производная 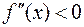, следовательно здесь функция выпукла, на интервалах (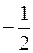, 1), (1, +¥) вторая производная 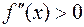, следовательно здесь функция вогнута. Так как при переходе через точку 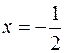вторая производная меняет знак, то 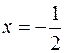— точка перегиба.

.

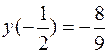8. Найдем точки пересечения графика функции с осями координат.

,

.

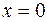
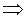
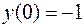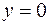
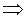
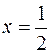Построение графика начнем с нанесения асимптот, то­чек пересечения с осями координат, экстремума, перегиба и фрагментов графика функции вблизи этих точек и асимптот.

В окончательном виде график изображен на рисунке.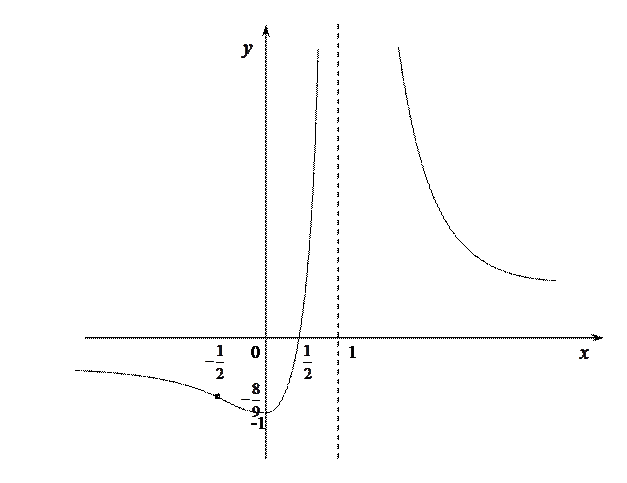

ЛИТЕРАТУРА

1. Воднев В. Т. и др. Основные математические формулы: Справочник /
В. Т. Воднев, А. Ф. Наумович, Н. Ф. Наумович; Под ред. Ю. С. Богданова.— 3-е изд., перераб. и доп.— Мн.: Вышэйшая школа, 1995.—380 с: ил.

2. Герасимович А. И. и др. Математический анализ: Справ. пособие.
В 2 ч. Ч.2 /А. И. Герасимович, Н. П. Кеда, М. Б. Сугак.—Мн.: Вышэйшая школа, 1990.— 272 с: ил.

3. Гусак А. А. Высшая математика. Т. 2: [Учеб. пособие для естеств. спец. университетов.— 2-е изд., перераб. и доп.— Мн: Изд-во БГУ, 1983.—462 с.

4. Гусак А.А. Пособие к решению задач по высшей математике. - Мн.: Вышэйшая школа, 1967.

5. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. - М.; Высшая школа, 1974.

6. Жевняк P.M., Карпук А.А. Высшая математика. Функция многих переменных. Интегральное исчисление. - Мн.: Вышэйшая школа, 1993.

7. Пискунов Н.С. Дифференциальное и интегральное исчисление, т.1-
М.: Наука, 1976.

8. Руководство к решению задач по высшей математике. /Под ред.
Гурского Е.И. Части 1 и 2. - Мн.: Вышэйшая школа, 1989.

9. Сборник задач по общему курсу высшей математики. Под редакцией Яблонского А.И. Мн.: Вышэйшая школа. 1994 г.