2015-06-04
324
Рассмотрим свойства неопределенного интеграла, вытекающие из его определения.
1. Производная от неопределенного интеграла равна подынтегральной функции, дифференциал от неопределенного интеграла равен подынтегральному выражению:
, 
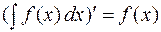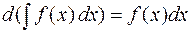
Доказательство. Пусть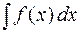 
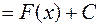. Тогда
,
.
⊠
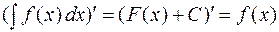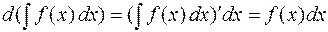2. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
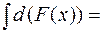
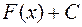
Доказательство. Действительно, так как
.
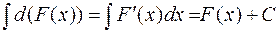Например,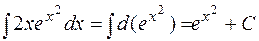 
.
⊠
3. Постоянный множитель можно выносить за знак неопределенного интеграла:
.
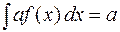
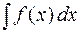Доказательство. Действительно, пусть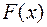 
— первообразная функции 
: | 
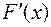= . Тогда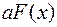 
— первообразная функции 
: 
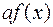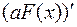
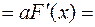
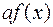. Отсюда следует, что
.
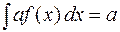
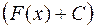
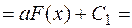
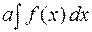где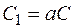 
.
⊠
4. Неопределенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от этих функций.
Доказательство. Доказательство проведем для двух функций. Пусть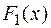 
и 
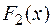— первообразные функци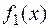й 
и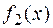 
: 
, 
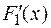
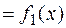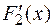
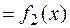. Тогда функции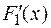 
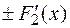являются первообразными функций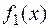 
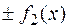. Следовательно,
⊠
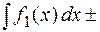
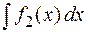
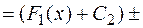
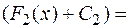
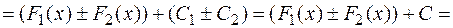
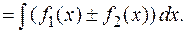
5. Если 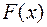— первообразная функции , то
.
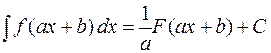Доказательство. Действительно,
.
⊠
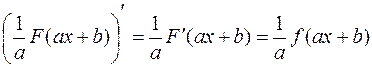6 (инвариантность формул интегрирования). Любая формула интегрирования сохраняет свой вид, если переменную интегрирования заменить любой дифференцируемой функцией этой переменной:
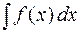
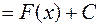
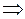
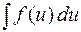
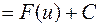
где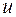 
— дифференцируемая функция.
В отличие от дифференциального исчисления, где, пользуясь таблицей производных, можно найти производную или дифференциал любой заданной функции, в интегральном исчислении нет общих приемов вычисления неопределенных интегралов, а разработаны лишь частные методы, позволяющие свести данный интеграл к табличному.
